Cắt mặt xung quanh của một hình nón theo 1 đường sinh và trải phẳng ra thành 1 hình quạt tròn AOB và cung AB có độ dài là 24π cm . Tính bán kính đáy của hình nón
.
.
.
Aii giúp mình với sắp thii rồi :v <3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
17 tháng 4 2017
Giải:
Độ dài l của cung hình quạt tròn bán kính 6 cm bằng chu vi đáy của hình nón:
l = 2 π.2 = 4 π
Áp dụng công thức tính độ dài cung trong x0 ta có:
l =
Suy ra: x0 = = 1200
CM
25 tháng 2 2018
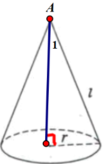
Cắt mặt xung quanh của một hình nón tròn xoay dọc theo một đường sinh rồi trải ra trên mặt phẳng ta được một nửa hình tròn bán kính R ⇒ đường sinh có độ dài bằng R và chu vi đường tròn đáy bằng nửa chu vi đường tròn bán kính R
CM
28 tháng 2 2019
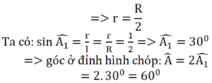
Chọn đáp án B
Phương pháp
Sử dụng công thức tính diện tích xung quanh hình nón S x q = π r l (với r là bán kính đáy, l là đường sinh hình nón).
Cách giải
Ta có diện tích xung quanh hình nón bằng
CM
21 tháng 4 2018
Chọn đáp án A
Phương pháp
Chu vi đường tròn đáy của hình nón chính là độ dài cung tròn của phần hình học được trải ra có bán kính 3cm.
Cách giải
Chu vi đường tròn đáy hình nón là:
17 tháng 12 2016
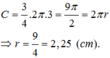
Dựng mặt phẳng (Q) chứa đường cao SO của hình chóp
Ta được thiết diện là tam giác SAB như hình vẽ
\(\Rightarrow OI=h;OA=OB=R;\widehat{ASO}=\widehat{BSO=\alpha}\)
(P) cắt (Q) qua giao tuyến MN, MN cắt SO tại điểm I \(\Rightarrow\) IM=IN=r (bán kính đường tròn (C) )
Tam giác SIN đồng dạng với tam giác SOB
\(\Rightarrow\frac{SI}{SO}=\frac{IN}{OB}\Leftrightarrow IN=\frac{SI.OB}{SO}=\frac{\left(SO-MO\right).OB}{SO}=\frac{\left(OB.cot\widehat{OSB}-MO\right).OB}{OB.cot\widehat{OSB}}\\ \Rightarrow r=\frac{Rcot\alpha-h}{Rcot\alpha}=1-\frac{h}{Rcot\alpha}\)
CM
17 tháng 4 2019
Khi khai triển mặt xung quanh của hình nón, ta được một hình quạt có bán kính bằng độ dài đường sinh.
Đề bài cho ta bán kính hình tròn chứa hình quạt là 16cm nên độ dài đường sinh của hình nón là 16cm.
Vậy chọn A.
