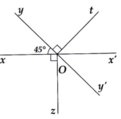
Cho góc xOy nhọn. Trên nửa mặt phẳng bờ là đường thẳng Oy không chứa cạnh Ox, kẻ Oz vuông góc Ox. Trên nửa mặt phẳng bờ là đường thẳng Ox không chứa cạnh Oy, kẻ Ot vuông góc Oy. Trên các tia Ot, Ox, Oy, Oz lấy các điểm A, B, C, D sao cho OA = OD; OC = OB
a) Chứng minh AC = DB
b) Gọi I là giao điểm của AC và DB. Chứng minh IA = ID; IB = IC và OI là tia phân giác của góc xOy

Xét tam giác ODB và tam giác OAC có: OD = OA
góc AOC = góc BOD (=90o)
OB = OC
=> tam giác ODB = tam giác OAC (c.g.c)=> AC = BD (2 cạnh t,ư )
b/Ta có góc DOC + COB = zOx = 90o
AOB + BOC = tOy = 90o
=> góc DOC = AOB mà OD =OA, OC = OB
=> tam giác ODC = OAB (c.g.c) => DC = AB (1)
Dễ có tam giác DCB = ABC (Vì BC chung, DC=AB,DB =AC )
=> góc CDB = CAB (2 góc t.ư) (2)
Dễ có tam giác CDA = BAD (vì AD chung, CD = AB, DB =AC ) => góc DCA = góc DBA (2 góc t.ư) (3)
Từ (1)(2)(3) => tam giác IDC =IAB (g.c.g)
=> ID = IA, IC = IB (cặp canh tương ứng )
Dễ có tam giác OIC = OIB (c.c.c)
=> góc COI = góc BOI (2 góc t.ư)
=> tia OI là phân giác của góc xOy