1. \(1+\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{99}}+\dfrac{1}{2^{100}}+\dfrac{1}{2^{100}}\)
2. So sánh: \(\dfrac{2008}{2009}+\dfrac{2009}{2010}\) và \(\dfrac{2008+2009}{2009+2010}\)
3. Rút gọn phân số: A = \(\dfrac{11+12+13+...+89}{21+22+23+...+99}\)
4. Tìm các cặp (x, y) nguyên thỏa mãn: \(\left|4y^2-3\right|+\left|5-2x\right|=2013\)
5. Tìm các số nguyên n để \(\dfrac{n+1}{n-2}\) có giá trị nguyên
6. Tìm \(x\in Z\) để \(B=\dfrac{x}{x+1}+\dfrac{2}{x+1}\) là số nguyên


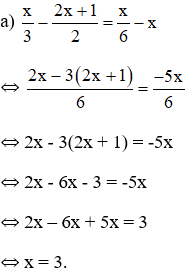
2, ta thấy:
\(\dfrac{2008}{2009}< \dfrac{2008}{2009+2010}\left(1\right)\)
\(\dfrac{2009}{2010}< \dfrac{2009}{2009+20010}\left(2\right)\)
từ (1) và (2) cộng vế với vế ta đc :\(\dfrac{2008}{2009}+\dfrac{2009}{20010}< \dfrac{2008}{2009+2010}+\dfrac{2009}{2009+2010}=\dfrac{2008+2009}{2009+2010}\)