vẽ đồ thị các hàm số sau :
a. y=4x+1
b. y=\(\dfrac{3}{x}\)
c. y=7-5x
d. y=-3x
nhanh nhé !
thanks !
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
SG
1
18 tháng 3 2018
- Plot y = 4*x + 1
- Plot y = 3/x
- Plot y = 3 – 5*x
- Plot y = 3*x
28 tháng 2 2022
Bài 3:
a: Thay x=3 vào y=-2x, ta được:
\(y=-2\cdot3=-6\)
b: Thay x=1,5 vào y=-2x, ta được:
\(y=-2\cdot1.5=-3< >3\)
Do đó: B(1,5;3) không thuộc đồ thị hàm số y=2x
CM
7 tháng 4 2019
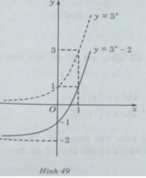
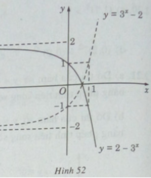
a) Đồ thị của hàm số y: y = 3 x − 2 nhận được từ đồ thị của hàm số y = 3 x bằng phép tịnh tiến song song với trục tung xuống dưới 2 đơn vị (H. 49)
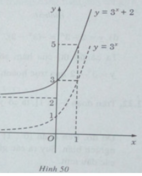
b) Đồ thị của hàm số y = 3 x + 2 nhận được từ đồ thị của hàm số y = 3 x bằng phép tịnh tiến song song với trục tung lên phía trên 2 đơn vị (H. 50)
c)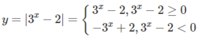 
Do đó, đồ thị của hàm số y = | 3 x − 2| gồm:
- Phần đồ thị của hàm số y = 3 x − 2 ứng với 3 x – 2 ≥ 0 (nằm phía trên trục hoành).
- Phần đối xứng qua trục hoành của đồ thị hàm số y = 3 x − 2 ứng với 3 x – 2 < 0.
Vậy đồ thị của hàm số y = | 3 x − 2| có dạng như hình 51.
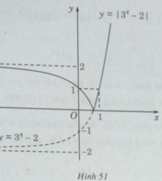
Ta có đồ thị của hàm số y = 2 − 3 x đối xứng với đồ thị cua hàm số y = 3 x – 2 qua trục hoành (H.52).
AG
0
MH
9 tháng 4 2017
a) =
=
.
b) =
=
.
c) =
=
.
d) y' =\(\dfrac{\left(x^2+7x+3\right)'\left(x^2-3x\right)-\left(x^2+7x+3\right)\left(x^2-3x\right)'}{\left(x^2-3x\right)^2}\)=\(\dfrac{\left(2x+7\right)\left(x^2-3x\right)-\left(x^2+7x+3\right)\left(2x-3\right)}{\left(x^2-3x\right)^2}\)=\(\dfrac{-2x^2-6x+9}{\left(x^2-3x\right)^2}\)
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 9 2021
a.
\(y'=-\dfrac{3}{2}x^3+\dfrac{6}{5}x^2-x+5\)
b.
\(y'=\dfrac{\left(x^2+4x+5\right)'}{2\sqrt{x^2+4x+5}}=\dfrac{2x+4}{2\sqrt{x^2+4x+5}}=\dfrac{x+2}{\sqrt{x^2+4x+5}}\)
c.
\(y=\left(3x-2\right)^{\dfrac{1}{3}}\Rightarrow y'=\dfrac{1}{3}\left(3x-2\right)^{-\dfrac{2}{3}}=\dfrac{1}{3\sqrt[3]{\left(3x-2\right)^2}}\)
d.
\(y'=2\sqrt{x+2}+\dfrac{2x-1}{2\sqrt{x+2}}=\dfrac{6x+7}{2\sqrt{x+2}}\)
e.
\(y'=3sin^2\left(\dfrac{\pi}{3}-5x\right).\left[sin\left(\dfrac{\pi}{3}-5x\right)\right]'=-15sin^2\left(\dfrac{\pi}{3}-5x\right).cos\left(\dfrac{\pi}{3}-5x\right)\)
g.
\(y'=4cot^3\left(\dfrac{\pi}{6}-3x\right)\left[cot\left(\dfrac{\pi}{3}-3x\right)\right]'=12cot^3\left(\dfrac{\pi}{6}-3x\right).\dfrac{1}{sin^2\left(\dfrac{\pi}{3}-3x\right)}\)
