Cho tam giác nhọn ABC, các đường cao BD, CE cắt nhau tại H. C/m: BC2 = BH . BD + CH . CE
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
10 tháng 4 2018
Gợi ý: Gọi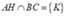 
, chứng minh được AK ^ BC.
Áp dụng cách làm tương tự 4A suy ra ĐPCM
26 tháng 7 2018
Kẻ \(HM\perp BC\)
Xét \(\Delta BHM\) và \(\Delta BCD\) ta có:
\(\widehat{BMH}=\widehat{BDC}=90^o\)
\(\widehat{CBD}\) chung
\(\Rightarrow\Delta BHM\sim\Delta BCD\left(g.g\right)\)
\(\Rightarrow\dfrac{BM}{BD}=\dfrac{BH}{BC}\Rightarrow BM\times BC=BH\times BD\left(1\right)\)
Xét \(\Delta CMH\) và \(\Delta CEB\) ta có:
\(\widehat{BCE}\) chung
\(\widehat{CMH}=\widehat{CEB}=90^o\)
\(\Rightarrow\Delta CMH\sim\Delta CEB\left(g.g\right)\)
\(\Rightarrow\dfrac{CH}{CB}=\dfrac{CM}{CE}\Rightarrow CM\times CB=CH\times CE\left(2\right)\)
Cộng 2 vế của (1)(2) lại với nhau ta đc:
\(BM.BC+CM.CB=BH.BD+CH.CE\)
\(\Leftrightarrow BC\left(BM+CM\right)=BH.BD+CH.CE\)
\(\Rightarrow BC^2=BH.BD+CH.CE\left(đcpcm\right)\)
Vậy..............
6 tháng 5 2016
a) Chứng minh tam giác AED đông dang tam giác ACB
b) Kẻ HI vuông góc BC
Có BHxBD+CHxCE=BC^2 bằng xét 2 cặp tam giác đông dạng.
21 tháng 6 2023
1:
a: góc AEH+góc ADH=180 độ
=>AEHD nội tiếp
b: góc BEC=góc BDC=90 độ
=>BEDC nội tiếp
c: BEDC nội tiếp
=>góc EBD=góc ECD
d: Xét ΔABC có
BD,CE là đường cao
BD cắt CE tại H
=>H là trực tâm
=>AH vuông góc BC
B1
1 tháng 8 2017
Cho tam giác nhọn ABC có hai đường cao BD và CE căt nhau tại H .
Chứng minh rằng : BC^2=BH.BD+CH.CE
Bài này em có thể giải như sau
1)1) Ta có:
△CDH∼△ACE (g.g)△CDH∼△ACE (g.g)
⇒CHAE=CDAC⇒CH.AC=AE.CD=AB.AE⇒CHAE=CDAC⇒CH.AC=AE.CD=AB.AE
△ADH∼△ACF (g.g)△ADH∼△ACF (g.g)
⇒ADAC=AHAF⇒AH.AC=AD.AF⇒ADAC=AHAF⇒AH.AC=AD.AF
Do đó: AC2=AH.AC+CH.AC=AB.AE+AD.AFAC2=AH.AC+CH.AC=AB.AE+AD.AF
2)2) Dựng HFHF vuông góc BC.BC. Ta có:
△BFH∼△BDC△BFH∼△BDC
⇒BFBD=BHBC⇒BF.BC=BD.BH⇒BFBD=BHBC⇒BF.BC=BD.BH
△CFH∼△CEB△CFH∼△CEB
⇒CF/CE=CHCB⇒CF.BC=CE.CH⇒CFCE=CHCB⇒CF.BC=CE.CH
Do đó: BC^2=BF.BC+CF.BC=BD.BH=CE.CH
các dấu kí tự bạn tự thêm nhé
a. Vẽ AM (HM) cũng vuông với BC
Xét tam giác BHM và BCD có:
góc BEH = góc BCD = 90o
góc CBD chung
Do đó tam giác BHM~BCD ( g.g)
=> \(\dfrac{BM}{BD}=\dfrac{BH}{BC}\Rightarrow BM.BC=BH.BD\) (1)
Xét tam giác CMH và CEB có:
góc BCE chung
góc HMC = góc CEB = 90o
Do đó tam giác CMH~CEB (g.g)
=> \(\dfrac{CH}{CB}=\dfrac{CM}{CE}\Rightarrow CM.CB=CH.CE\) (2)
Từ (1) và (2) cộng vế theo vế ta được:
BM.BC +CM.CB = BH.BD+CH.CE
=> (BM + CM) .BC = BH . BD + CH . CE
=> BC2 = BH . BD + CH . CE (đpcm)
AH cắt BC tại F thì AF _|_ BC
Tg HFC~ Tg BEC
=> HC/BC = FC/EC
=> HC.EC = BC.FC
Tương tự : BH.BD = BF.BC
Suy ra : BH.BD + EC.HC = BC(BF + FC) = BC^2 Hay BC^2 = BH . BD + CH . CE