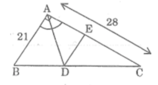
Cho tam giác ABC vuông tại A có đường trung tuyến AM và đường phân giác BD ( D \(\in\) AC ) biết AB = 6cm, AC = 8cm. Đường thẳng qua D và song song với BC cắt AB tại E.
a, Tính độ dài BC,AD,DC,DE.
b, Gọi I là giao điểm của AM và DE. Chứng minh ID = IE


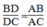 (t/chất đường phân giác)
(t/chất đường phân giác)
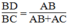
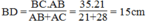
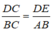 (Hệ quả định lí Ta-lét)
(Hệ quả định lí Ta-lét)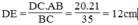
a, - Áp dụng định lý pi - ta go vào tam giác ABC vuông tại A có :
\(BC=\sqrt{AB^2+AC^2}=10\left(cm\right)\)
- Ta có : AD là phân giác của góc ACB .
=> \(\frac{BA}{AD}=\frac{BC}{DC}\) = \(\frac{6}{AD}=\frac{10}{DC}\)
- Áp dụng tính chất dãy tỉ số bằng nhau ta được :
\(\frac{6}{AD}=\frac{10}{DC}=\frac{16}{AC}=\frac{16}{8}=2\)
=> \(\left\{{}\begin{matrix}AD=3\\DC=5\end{matrix}\right.\) ( cm )