Câu hỏi xét tính đơn điệu của hàm số
Giúp mình với mình cần gấp ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
LN
1
Những câu hỏi liên quan
NT
0
MM
1
27 tháng 5 2021
a) Hàm số xđ <=> \(1+cos2x>0\) \(\Leftrightarrow cos2x\ne-1\) \(\Leftrightarrow\)\(2cos^2x-1\ne-1\)
\(\Leftrightarrow cosx\ne0\) \(\Leftrightarrow x\ne\dfrac{\pi}{2}+k\pi\left(k\in Z\right)\)
b)Hàm số xđ <=> \(1-sinx>0\) \(\Leftrightarrow sinx\ne1\) \(\Leftrightarrow x\ne\dfrac{\pi}{2}+k2\pi\left(k\in Z\right)\)
c) Hàm số xđ <=> \(sinx+cos5x\ne0\)
\(\Leftrightarrow sinx\ne-cos5x\)
\(\Leftrightarrow cos\left(\dfrac{\pi}{2}-x\right)\ne cos\left(\pi-5x\right)\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{\pi}{2}-x\ne\pi-5x+k2\pi\\\dfrac{\pi}{2}-x\ne-\pi+5x+k2\pi\end{matrix}\right.\) (\(k\in Z\))
\(\Leftrightarrow\left\{{}\begin{matrix}x\ne\dfrac{\pi}{8}+\dfrac{k\pi}{2}\\x\ne\dfrac{\pi}{4}-\dfrac{k\pi}{3}\end{matrix}\right.\)(\(k\in Z\))
d) Hàm số xđ <=> \(sinx-\sqrt{3}cosx\ne0\)
\(\Leftrightarrow2.sin\left(x-\dfrac{\pi}{3}\right)\ne0\) \(\Leftrightarrow x\ne\dfrac{\pi}{3}+k\pi\left(k\in Z\right)\)
e) Hàm số xđ <=> \(\left(sinx+1\right).cosx\ne0\)
\(\Leftrightarrow\left\{{}\begin{matrix}sinx\ne-1\\cosx\ne0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ne-\dfrac{\pi}{2}+k2\pi\\x\ne\dfrac{\pi}{2}+k\pi\end{matrix}\right.\) (\(k\in Z\)) \(\Rightarrow x\ne\dfrac{\pi}{2}+k\pi\) (Hai họ nghiệm trùng nhau nên e tổng hợp lại, e nghĩ thế)
f) Hàm số xđ <=> \(\left\{{}\begin{matrix}\left(1-tanx\right)\left(1-cotx\right)\ne0\\sinx\ne0\\cosx\ne0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}tanx\ne1\\cotx\ne1\\sinx.cosx\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}sinx\ne cosx\\\dfrac{1}{2}.sin2x\ne0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}sinx\ne sin\left(\dfrac{\pi}{2}-x\right)\\2x\ne k\pi\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ne\dfrac{\pi}{2}-x+k2\pi\\x\ne\dfrac{\pi}{2}+x+k2\pi\\x\ne\dfrac{k\pi}{2}\end{matrix}\right.\)(\(k\in Z\))
\(\Leftrightarrow\left\{{}\begin{matrix}x\ne\dfrac{\pi}{4}+k\pi\\0\ne\dfrac{\pi}{2}+k2\pi\\x\ne\dfrac{k\pi}{2}\end{matrix}\right.\)(\(k\in Z\)) \(\Leftrightarrow\left\{{}\begin{matrix}x\ne\dfrac{\pi}{4}+k\pi\\x\ne\dfrac{k\pi}{2}\end{matrix}\right.\)(\(k\in Z\))
13 tháng 11 2016
- Vì quyên lợi cá nhân.
- Đồng loạt và khá triệt để
@sen phùng em làm đúng 100% đó
11 tháng 4 2021
*Dân chủ: Dân chủ là một phương pháp ra quyết định tập thể trong đó mọi thành viên đều có quyền ngang nhau khi tham gia ra quyết định. ... Theo nhà khoa học chính trị Larry Diamond, chế độ dân chủ bao gồm bốn yếu tố chính: Một hệ thống chính trị cho việc lựa chọn và thay thế các chính phủ thông qua bầu cử tự do và công bằng.
*Cộng hòa: là một hình thức chính phủ trong đó quốc gia được coi là "vấn đề công cộng" thông qua các pháp luật và hiến pháp cũng như các quy định chung và chế độ dân chủ, không phải là mối quan tâm riêng tư ...
Ý ghĩa ở đây nói Việt Nam là một nước : Tức là nói đến Bộ máy nhà nước có sự phân quyền giữa ba nhánh quyền lực lập pháp, hành pháp, và tư pháp. Nó khác hoàn toàn với chuyên chế hay độc tài. Dân chủ là thể thức mà ở dó người dân có khả năng tham gia quyết định các chính sách của một quốc gia hay tham gia thành lập bộ máy nhà nước thông qua bầu cử. Có 2 hình thức dân chủ là Dân chủ trực tiếp và dân chủ gián tiếp. Tuy nhiên, tùy theo từng nước và hoàn cảnh quốc gia mà thể chế dân chủ phát triển đến mức độ nào.
AH
Akai Haruma
Giáo viên
12 tháng 8 2021
Lời giải:
$y=(3x+6)^5(-x+1)$
$y'=-9(3x+6)^4(2x-1)$
$y'=0\Leftrightarrow x=-2$ hoặc $x=\frac{1}{2}$
Lập BBT ta thấy hàm đồng biến trên $(-\infty; \frac{1}{2})$ và nghịch biến trên $(\frac{1}{2};+\infty)$
PT
1
CM
13 tháng 7 2019
Xét hàm số:
y
=
4
-
x
2
x
+
3
m
TXĐ: R \ {−3m/2}
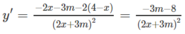
+) Nếu m < −8/3, y′ > 0 suy ra hàm số đồng biến trên các khoảng 
+) Nếu m > −8/3, y′ < 0 suy ra hàm số nghịch biến trên các khoảng
+) Nếu m = −8/3 thì y = −1/2 khi x ≠ 4
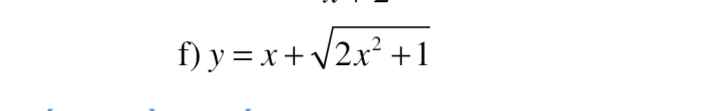
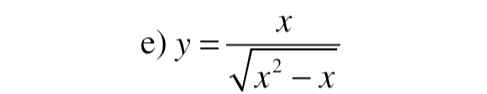
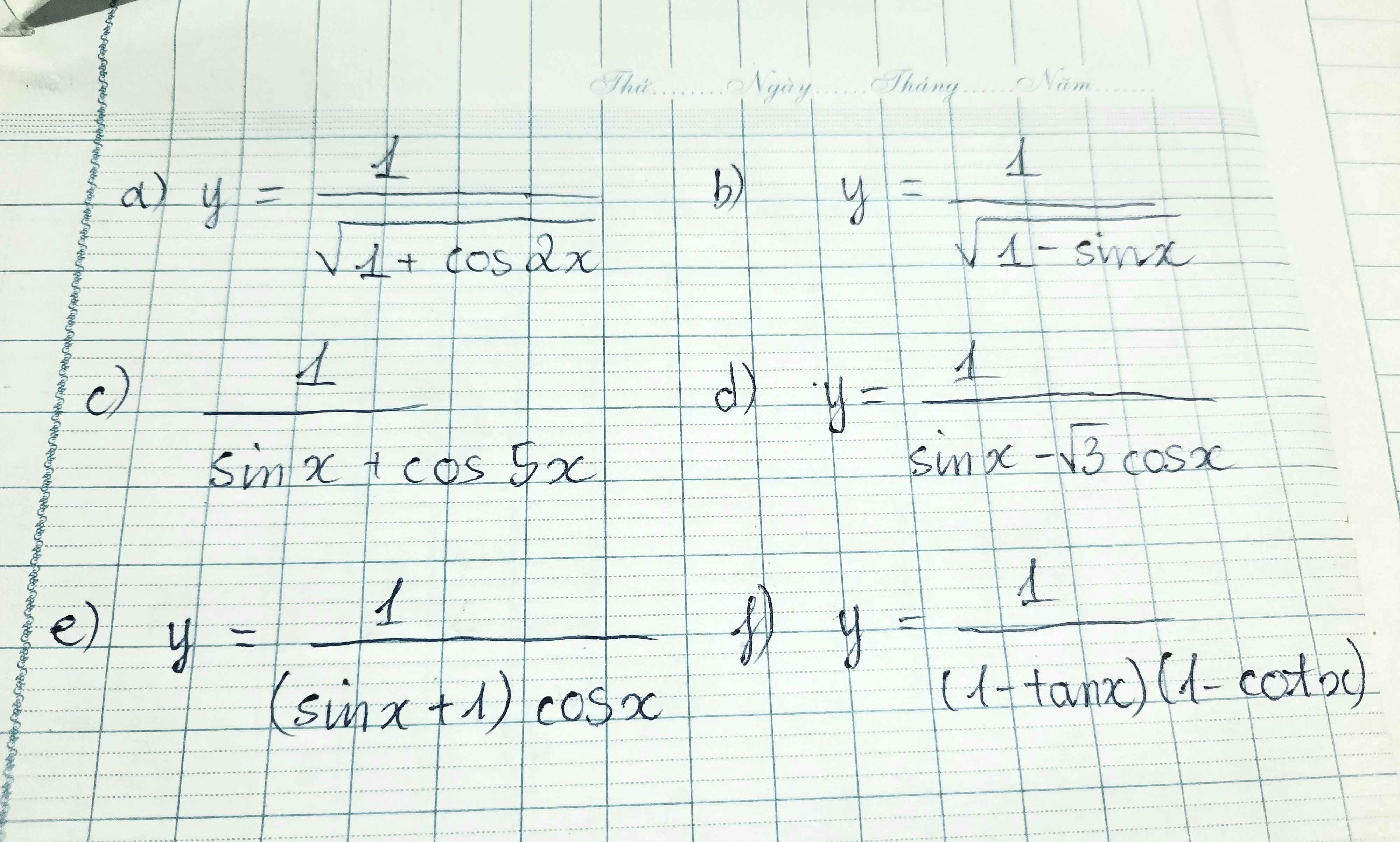
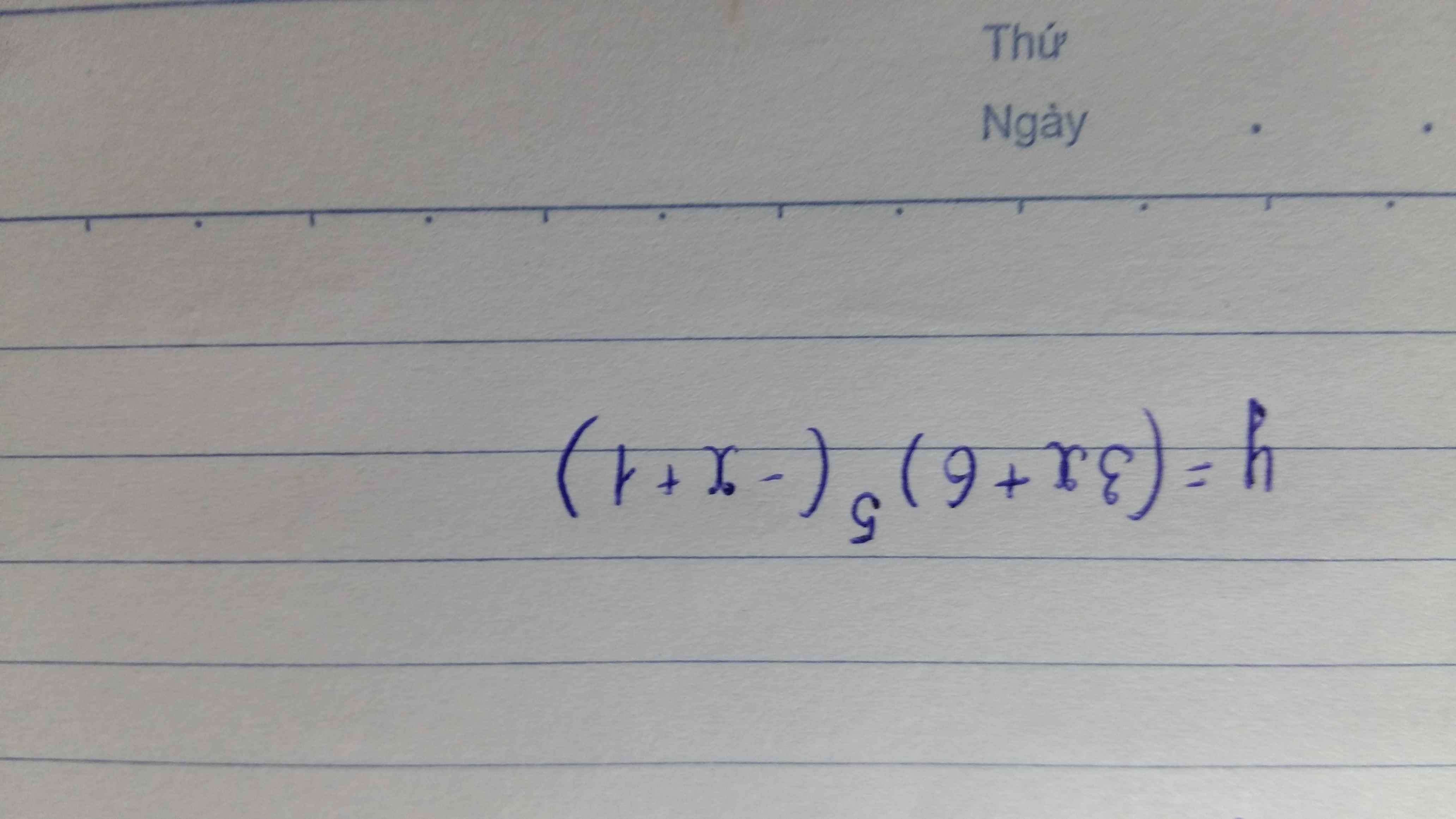
a.
\(y'=4x^3-4x=4x\left(x^2-1\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\x=-1\\x=1\end{matrix}\right.\)
Dấu y' trên trục số:
Hàm đồng biến trên các khoảng \(\left(-1;0\right)\) và \(\left(1;+\infty\right)\)
Hàm nghịch biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(0;1\right)\)
b.
\(y'=x^2+6x-7=0\Rightarrow\left[{}\begin{matrix}x=-7\\x=1\\\end{matrix}\right.\)
Dấu của y' trên trục số:
Hàm đồng biến trên các khoảng \(\left(-\infty;-7\right)\) và \(\left(1;+\infty\right)\)
Hàm nghịch biến trên \(\left(-7;1\right)\)
cô ơi giúp em bài này đc k cô