Hai ôtô chuyển động thẳng đều xuất phát cùng một lúc từ hai điểm A và B trên một đường thẳng cách nhau 20km. Xe 1 xuất phát từ A chạy về B, xe 2 xuất phát từ B chạy cùng chiều xe 1. Vận tốc xe 1 là 50 km/h, xe 2 là 30 km/h. Hỏi sau bao lâu xe 1 gặp xe 2?Tính quãng đường mỗi xe đi được khi gặp nhau và vẽ đồ thị (x-t) của hai xe.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Gọi thời gian xuất phát là to, điểm gốc tại A, chiều dương là chiều từ A đến B .
- Theo bài ra ta có : \(\left\{{}\begin{matrix}x_1=30t\\x_2=L+40t\\x_{3.1}=L-50t\end{matrix}\right.\)
- Ta có : Khi xe 1 và xe 3 gặp nhau thì tổng quãng đường đi được là AB.
\(\Rightarrow80t=L\)
\(\Rightarrow t=\dfrac{L}{80}\)
=> Hai xe gặp nhau lại điểm cách A : \(\dfrac{30L}{80}=\dfrac{3L}{8}\left(km\right)\)
- Xét quá trình từ sau khi xe 1 gặp xe 3 :\(\left\{{}\begin{matrix}x_1=\dfrac{3L}{8}+30t^,\\x_2=40.\dfrac{L}{80}+L+40t^,\\x_3=\dfrac{3L}{8}+50t^,\end{matrix}\right.\)
- Để xe 2 đuổi kịp xe 3 thì \(\dfrac{3}{2}L+40t^,=\dfrac{3}{8}L+50t^,\)
Lại có : \(t=\dfrac{L}{80}\)
\(\Rightarrow t+t^,=0,09=\dfrac{L}{80}+t^,\)
- Giair hệ ta được : \(\left\{{}\begin{matrix}L=0,72\left(km\right)\\t^,=0,081\left(h\right)\\t=0,009\left(h\right)\end{matrix}\right.\)
b, Ta có : \(d_{3-1}=\dfrac{3}{8}L+50t^,-\dfrac{3}{8}L-30t^,=1,62\left(km\right)\)
Vậy ,....
- Gọi chiều dương là chiều từ người đi bộ hướng tới người đi xe đạp , thời gian gốc là to, điểm mốc tại người đi bộ và khoảng cách giữa người đi bộ và đi xe đạp là x0 ( km, x > 0 ) và 3 người xe đạp, bộ, xe máy lần lượt là 1,2,3 .
- Theo bài ra ta có : \(\left\{{}\begin{matrix}x_1=x_0+20t\\x_2=vt\\x_3=-2x_0+60t\end{matrix}\right.\)
- Để 3 người cùng gặp nhau tại 1 điểm .
=> \(x_1=x_2=x_3=x\)
\(\Rightarrow x_0=\dfrac{40}{3}t\)
\(\Rightarrow x=\dfrac{100}{3}t=vt\)
\(\Rightarrow v=\dfrac{100}{3}\left(km/h\right)\)
Vậy ...

Giải:
a; Chọn chiều dương là chiều chuyển động từ A đến B, gốc tọa độ tại A, gốc thời gian là lúc hai xe xuất phát
phương trình chuyển động của hai xe x = x 0 + v t
Đối với xe chuyển động từ A : x 0 A = 0 ; v A = 60 k m / h ⇒ x A = 60 t
Đối với xe chuyển động từ B : x 0 B = 20 k m ; v B = 40 k m / h ⇒ x B = 20 + 40 t
b; Ta có bảng (x,t)
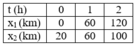
Đồ thị:
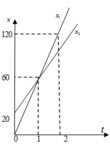
c; Dựa vào đồ thị ta thấy 2 xe gặp nhau ở vị trí cách A 60km và thời điểm mà hai xe gặp nhau 1h

Hướng dẫn :
a/ Chọn chiều dương là chiều chuyển động từ A đến B, gốc tọa độ tại A, gốc thời gian là lúc hai xe xuất phát
phương trình chuyển động của hai xe
Đối với xe chuyển động từ A :
Đối với xe chuyển động từ B :
b/ Ta có bảng ( x, t )
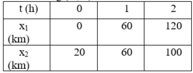
Đồ thị:
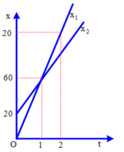
c/ Dựa vào đồ thị ta thấy 2 xe gặp nhau ở vị trí cách A 60km và thời điểm mà hai xe gặp nhau 1h.

a)
- Chọn gốc tọa độ O là vị trí ô tô bắt đầu đuổi theo xe khách và mốc thời gian là thời điểm ô tô đang ở O.
- Phương trình chuyển động của hai xe là:
+ Ô tô: \(x_1=v_1.t=60t\)
+ Xe khách: \(x_2=x_0+v_2.t=20+40t\)b) - Lập bảng biến thiên (tớ làm cái này chứ ít thấy người viết cái này bạn nhé)
| \(t\left(h\right)\) | \(0\) | \(1\) |
| \(x_1\left(km\right)\) | \(0\) | \(60\) |
| \(x_2\left(km\right)\) | \(20\) | \(60\) |
=> Ta vẽ được đồ thị của 2 xe như sau:

c) Dựa vào đồ thị cho ta biết thời điểm 2 xe gặp nhau là sau 1 giờ và tại vị trí có toạ độ \(60km\)
Bạn chưa tính x thì làm sao lập đồ thị được, bảng biến thiên có bị thiếu ko, thấy hơi kì

chon \(Ox\equiv AB,O\equiv A,\) chieu(+) A->B, moc tgian luc xuat phat
a,\(\Rightarrow\left\{{}\begin{matrix}xA=50t\\xB=180-40t\end{matrix}\right.\)
b,\(\Rightarrow xA=xB=>t=2h\) vi tri gap nhau cach A 100km
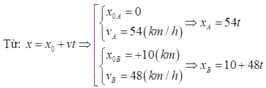
Chọn gốc tọa độ O trùng A
Chọn chiều dương trục Ox: từ A đến B
Phương trình chuyển động mỗi xe
\(x_A=50t\left(km,h\right)\)
\(x_B=20+30t\left(km,h\right)\)
Khi 2 xe gặp nhau:
\(x_A=x_B\Rightarrow50t=20+30t\Leftrightarrow t=1\left(h\right)\)
Vậy sau 1 h thì 2 xe gặp nhau và quãng đường mà xe 1 là\(50\cdot1=50\left(km\right)\) và xe 2 là \(30\cdot1=30\left(km\right)\)
< đồ thị bạn tự vẽ nha>;-;