Chứng minh rằng với mọi số nguyên n thì \(n^2+11n+39\) không chia hết cho 49.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
A
1
CH
Cô Hoàng Huyền
Admin
VIP
15 tháng 8 2018
a) Em tham khảo tại đây nhé:
Câu hỏi của VRCT_Ran love shinichi - Toán lớp 8 - Học toán với OnlineMath
PT
7
8 tháng 8 2015
bạn sai đề rồi:
chứng minh với mọi số nguyên n thì n^2+11n+39 không chia hết cho 49
Ta có:
giả sử: A= n^2 + 11n + 39 chia hết cho 49 => A chia hết cho 7
mà : n^2 + 11n + 39 = (n+9)(n+2) +21 chia hết cho 7
=> (n+9)(n+2) chia hết cho 7
lại có: (n+9) - (n+2) = 7 nên (n+9) và (n+2) đồng thời chia hết cho 7
=>(n+9)(n+2) chia hết cho 49
mà: (n+9)(n+2) +21 chia hết cho 49
=> 21 chia hết cho 49 vô lí => đpcm
8 tháng 8 2015
https://vn.answers.yahoo.com/question/index?qid=20091017203207AAoSfKD
ban vao link nay thi se co cau tra loi
FF
5
28 tháng 12 2017
Đặt A=n2+11n+39
Giả sử n2+11n+39 chia hết cho 49 thì A chia hết cho 49 => A cũng chia hết cho 7
Ta có A=n2+11n+39=n2+9n+2n+18+21 = n(n+9)+2(n+9)+21 =(n+9)(n+2)+21
Nhận thấy( n+9)-(n+2)=7
=>Đồng thời (n+9) và (n+2) chia hết cho 7 => (n+9)(n+2) chia hết cho 49
Ta cũng có A chia hết cho 49 mà 21 ko chia hết cho 49 ( vô lí )
Vậy n2+11n+39 ko chia hết cho 49
KV
5
15 tháng 11 2016
giả sử: A= n^2 + 11n + 39 chia hết cho 49 => A chia hết cho 7
mà : n^2 + 11n + 39 = (n+9)(n+2) +21 chia hết cho 7
=> (n+9)(n+2) chia hết cho 7
lại có: (n+9) - (n+2) = 7 nên (n+9) và (n+2) đồng thời chia hết cho 7
=>(n+9)(n+2) chia hết cho 49
mà: (n+9)(n+2) +21 chia hết cho 49
=> 21 chia hết cho 49 vô lí => đpcm
Bài 2: A=3^ (2*n) + 3^n + 1
n không chia hết cho 3 nên ta xét 2 trường hợp:
* n =3k +1:
A = 3^ (6k + 3) + 3^(3k +1) +1= 9.27^2k +3.27^ +1
= 9.(26+1)^2k + 3.(26 +1)^k +1
= 9(2.13 +1)^2k + 3.(2.13 +1)^k +1
A đồng dư với (9 +3 +1)= 13 theo đồng dư 0 theo (mod 13)
vậy A chia hết cho 13.
( Mình giải thích thêm nhé:
(2.13 +1)^2k chia cho 13 dư 1
=> 9(2.13 +1)^2k chia cho 13 dư 9
(2.13 +1)^k chia 13 dư 1
=> 3.(2.13 +1)^k chia 13 dư 1
=> A chia 13 dư 9 + 3 +1 = 13
A = 13.k +13 với k nguyên
A/13 = k + 1 la số nguyên => A chia hết cho 13
khi triển khai (x+1)^n = thì các hạng tử đều chứa x trừ hạng tử cuối = 1 nên (x+1)^n chia cho x dư 1.)
* n = 3k +2:
A = 3^(6k +4) + 3^(6k +2) +1=81.27^2k +9.27^k +1
= 81.(2.13+1)^2k + 9(2.13 +1)^k +1
A đồng dư với ( 81 + 9 +1) = 91 đồng dư 0 theo (mod 13)
vậy A chia hết cho 13
HT
7
NV
0
DN
2
21 tháng 2 2017
CM bằng cách thế số vào n
Thay n=169,ta đc
1692+11.169+2=30422
Ta thấy : 30422 ko chia hết cho 12769
\(\Rightarrow\)\(n^2+11n+2\)ko chia hết cho 12769 với mọi n
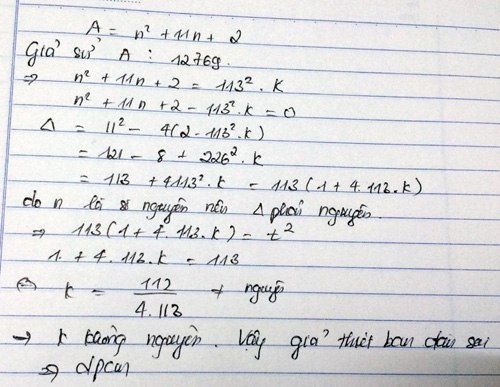
Giả sử \(n^2+11n+39⋮49\) \(\Rightarrow4n^2+44n+156⋮49\)
\(\Rightarrow4n^2+44n+156⋮7\) \(\Leftrightarrow4n^2+2.2n.11+121+35⋮7\)
\(\Leftrightarrow\left(2n+11\right)^2+35⋮7\) mà \(35⋮7\) nên \(\left(2n+11\right)^2⋮7\) mà 7 là số nguyên tố
\(\Rightarrow\left(2n+11\right)^2⋮49\) \(\Rightarrow4n^2+4n+121⋮49\) mà
\(4n^2+4n+121+35⋮49\) nên \(35⋮49\) => vô lý vậy điều giả sử là sai
vậy n^2+11n+39 không chia hết cho 49