Cho tam giác ABC có diện tích bằng 126 m2. Trên BC kaasy E sao cho BE=2EC. Trên AB lấy D sao cho AD=DB. Trên CA lấy F sao cho CF=3FA. Các đoạn thẳng CD, BF, AE cắt nhau tại M,N,P. Tính diện tích MNP.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
3 tháng 12 2017
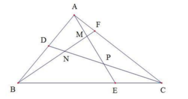
CPE = 1/3 CPB = 1/3 CPA=1/4 CAE=1/8 ABC
BND=1/2 BNA=1/6 BNC=1/7 BCD=1/14ABC
AMF=1/4 AMC=1/8 ABM= 1/9 ABF=1/36 ABC
AMND=ABF – BND – AMF
=1/4 ABC = 1/14 ABC = 1/36 ABC= 7/42 ABC
BEPD= BCD = CPE
= ½ ABC – 1/8 ABC = 3/8 ABC
MNP = ABC – AEC – BEPD – AMND
= ABC – 1/3 ABC – 3/8 ABC – 7/42 ABC
= 1/8 ABC
12 tháng 2 2020
Ta có : \(S_{MNP}=S_{ABC}-S_{APC}-S_{CBM}-S_{ABN}\)
\(S_{APC}+S_{PEC}=S_{AEC}=\frac{1}{3}S_{ABC}\)
\(\Rightarrow S_{AEC}=\frac{1}{3}.126=42\left(cm^2\right)\)
Kẻ \(AH\perp CD,EK\perp CD\left(H,K\in CD\right)\)
Ta có : \(\frac{AH.DC}{2}==S_{ADC}=S_{BDC}=3.S_{DEC}=\frac{3}{2}.EK.DC\)
\(\Rightarrow AK=3EK\Rightarrow S_{ADC}=3S_{EPC}\)
\(\Rightarrow S_{EPC}=\frac{1}{4}S_{AEC}=\frac{1}{4}.42=10,5\left(cm^2\right)\)
\(\Rightarrow S_{APC}=42-10,5=31,5\left(cm^2\right)\)
Mà \(S_{CBM}=S_{BCD}-S_{BMD}\)
Tương tự
\(S_{BCD}=\frac{1}{2}.S_{ABC}=\frac{1}{2}.126=63\left(cm^2\right)\)
\(S_{BMC=54cm^2,}S_{ABN}=28cm^2\)
\(\Rightarrow S_{MNP}=126-31,5-54-28=12,5\left(cm^2\right)\)
10 tháng 1 2017
a/ Kẽ AG, DH lần lược vuông góc với BC tại G,H. BI, EJ lần lược vuông góc với AC tại I,J. CK, FL lần lược vuông góc với AB tại K,L
Tính \(S_{BCD}\)
Ta có: AG // DH
\(\Rightarrow\frac{DH}{AG}=\frac{BD}{BA}=\frac{1}{2}\)
\(\Rightarrow\frac{S_{BCD}}{S_{ABC}}=\frac{\frac{1}{2}.DH.BC}{\frac{1}{2}.AG.BC}=\frac{1}{2}\)
\(\Rightarrow S_{BCD}=\frac{S_{ABC}}{2}=\frac{126}{2}=63\)
Tính \(S_{CAE}\)
Ta có: EJ // BI
\(\Rightarrow\frac{EJ}{BI}=\frac{EC}{CB}=\frac{1}{3}\)
\(\Rightarrow\frac{S_{CAE}}{S_{ABC}}=\frac{\frac{1}{2}.EJ.AC}{\frac{1}{2}.BI.AC}=\frac{1}{3}\)
\(\Rightarrow S_{CAE}=\frac{S_{ABC}}{3}=\frac{126}{3}=42\)
Tính \(S_{ABF}\)
Ta có: FL // CK
\(\Rightarrow\frac{FL}{CK}=\frac{AF}{AC}=\frac{1}{4}\)
\(\Rightarrow\frac{S_{ABF}}{S_{ABC}}=\frac{\frac{1}{2}.FL.AB}{\frac{1}{2}.CK.AB}=\frac{1}{4}\)
\(\Rightarrow S_{ABF}=\frac{S_{ABC}}{4}=\frac{126}{4}=31,5\)
b/ Kẽ AQ, ER lần lượt vuông góc với DC tại Q,R
Ta có: \(S_{ACD}=S_{ABC}-S_{BCD}=126-63=63=S_{BCD}\)
\(\Rightarrow\frac{S_{ACD}}{S_{ECD}}=\frac{S_{BCD}}{S_{ECD}}=\frac{\frac{1}{2}.h_B.DC}{\frac{1}{2}.h_E.DC}=3\)
Xét \(\Delta ENP\approx\Delta AMP\)(\(\approx\)là đồng dạng)
\(\Rightarrow\frac{EP}{AP}=\frac{ER}{AQ}=\frac{S_{ECD}}{S_{ACD}}=\frac{1}{3}\)
\(\Rightarrow AP=3PE\)
Tương tự ta có:
\(\frac{BM}{MF}=?\)
\(\frac{CN}{ND}=??\)
c/ Ta có:
\(\frac{S_{CPE}}{S_{CAE}}=\frac{\frac{1}{2}.h_P.EC}{\frac{1}{2}.h_A.EC}=\frac{EP}{EA}=\frac{1}{4}\)
\(\Rightarrow S_{CPE}=\frac{S_{CAE}}{4}=\frac{42}{4}=10,5\)
Tương tự \(\Rightarrow S_{BND}\)và \(S_{AMF}\)
\(S_{MNP}=S_{BDC}+S_{CAE}+S_{ABF}-S_{BND}-S_{CPE}-S_{AMF}\)
