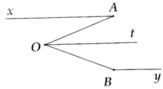
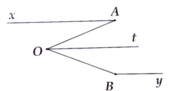
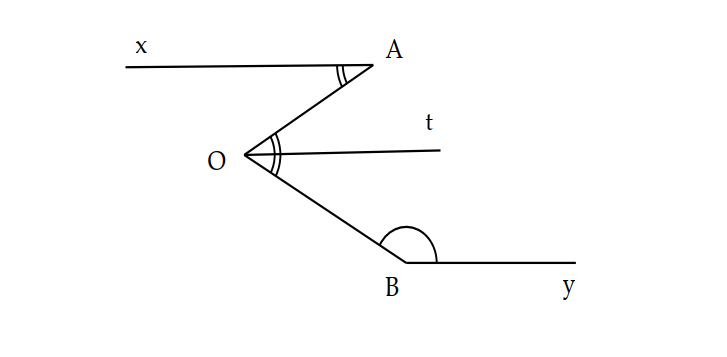
cho biet Ax song song voi By va OAx =45 do,OBy =135 do tinh AOB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
17 tháng 12 2018
Vì Ot là phân giác A O B ^ nên:
= A O t ^ = B O t ^ = 1 2 A O B ^ = 1 2 . 60° = 30°
=> x A O ^ = A O t ^ => Ax // Ot (1)
Lại có : t O A ^ + O B y ^ = 30° +150° = 180° => Ot // By. (2)
Từ (1) và (2), ta có Ax // By // Ot
22 tháng 9 2021
Ta có: \(\widehat{AOt}=\widehat{BOt}=\dfrac{\widehat{AOB}}{2}=60^0:2=30^0\)(do Ot là phân giác \(\widehat{AOB}\))
Ta có: \(\widehat{AOt}=\widehat{OAx}=30^0\)
Mà 2 góc này so le trong
=> Ax//Ot(1)
Ta có: \(\widehat{BOt}+\widehat{OBy}=30^0+150^0=180^0\)
Mà 2 góc này là 2 góc trong cùng phía
=> By//Ot(2)
Từ (1),(2) => đpcm
16 tháng 8 2021
kẻ tia Ot // Ax mà Ax//By
nên Qt//Ax//By
Ay//Ot
=>g xAO + g AOt=1800 ( hai góc trong cùng phía)
1050+ g AOt=1800
=>g AOt=1800-1050
=750
ta lại có gAOB=gAOt+gBOt
800=750+gBOt
=>gBOt=800-750=50
ta có Ot//By
=>gBOt+gOBy=1800(trong cùng phía)
50+gOBy=1800
=>gOBy=1800-50=1750
HP
26 tháng 12 2020
Phương trình đường thẳng ON có dạng \(y=a'x+b'\left(d'\right)\)
\(\left\{{}\begin{matrix}b'=0\\a'+b'=3\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}b'=0\\a'=3\end{matrix}\right.\Rightarrow y=3x\left(d'\right)\)
\(y=ax+b\left(d\right)\) đi qua \(E\left(2;-1\right)\Rightarrow2a+b=-1\left(1\right)\)
\(\left(d\right)//\left(d'\right)\Leftrightarrow\left\{{}\begin{matrix}a=3\\b\ne0\end{matrix}\right.\left(2\right)\)
\(\left(1\right),\left(2\right)\Rightarrow b=-7\)
\(\Rightarrow S=a^2+b^2=58\)
NT
0
30 tháng 6 2017
Ax // By <=> góc xAB + góc ABy = 180 độ (trong cùng phía)
<=> \(\alpha\)+ 4\(\alpha\)= 180 độ
<=> 5\(\alpha\)= 180 độ
<=> \(\alpha\)= 36 độ
Vậy \(\alpha\)= 36 độ để Ax // By
