Cho parabol (P): ax2+bx+c. Tìm tất cả các giá trị m để phương trình x2-x-m\(\sqrt{2}\)=0 có duy nhất 1 nghiệm
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
4 tháng 4 2021
a) Thay x=0 vào phương trình, ta được:
\(4\cdot0^2-2\cdot\left(2m+3\right)\cdot0+m+1=0\)
\(\Leftrightarrow m+1=0\)
hay m=-1
Áp dụng hệ thức Vi-et, ta có:
\(x_1+x_2=\dfrac{2\left(2m+3\right)}{4}\)
\(\Leftrightarrow x_1=\dfrac{2\cdot\left(-2+3\right)}{4}=\dfrac{2}{4}=\dfrac{1}{2}\)
Vậy: Khi m=-1 và nghiệm còn lại là \(x=\dfrac{1}{2}\)
CM
30 tháng 10 2017
Đáp án B.
Đặt t = log2 x,
khi đó m + 1 log 2 2 x + 2 log 2 x + m - 2 = 0
⇔ m + 1 t 2 + 2 t + m - 2 = 0 (*).
Để phương trình (*) có hai nghiệm phân biệt
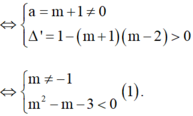
Khi đó gọi x1, x2 lần lượt hai nghiệm của phương trình (*).
Vì 0 < x1 < 1 < x2 suy ra
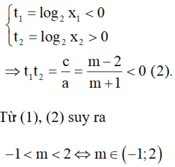
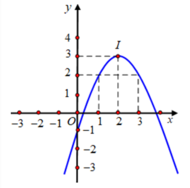
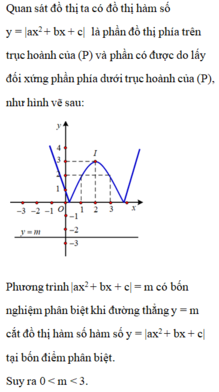
ai đó giúp mình với mình còn 3 tiếng nữa là tới hạn nộp bài rồi :(((