Với giá trị nào của x thì biểu thức :
P = \(\left(x-1\right)\left(x+2\right)\left(x+3\right)\left(x+6\right)\) đạt giá trị nhỏ nhất.
Tính giá trị nhỏ nhất ấy.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DN
12 tháng 1 2015
Ta thấy: |x-10| >= 0 (1); |x-10| >= 0 (2)
Cộng 2 bđt cùng chiều (1) và (2) ta được: |x-10| + |x-10| >= 0 <=> A= |x-10| + |x-10| -2 >= -2
=> minA = -2
Dấu đẳng thức xảy ra khi và chỉ khi x=10 và y=-100
Chắc v!! =)))
NV
5 tháng 9 2015
\(=8x+6x^2-12-9x\)
\(=6x^2-x-12=\left(-6\right)\left(-x^2+\frac{1}{6}x+2\right)\)
\(=\left(-6\right)\left[-x^2-2.\frac{1}{12}.\left(-x\right)+\left(\frac{1}{12}\right)^2-\left(\frac{1}{12}\right)^2+2\right]\)
\(=\left(-6\right)\left[\left(-x-\frac{1}{12}\right)^2+\frac{287}{144}\right]\)
\(=\left(-6\right)\left(-x-\frac{1}{12}\right)^2-\frac{287}{24}\ge-\frac{287}{24}\)
Vậy Min biểu thức = \(-\frac{287}{24}\) khi \(\left(-x-\frac{1}{12}\right)^2=0\Rightarrow-x-\frac{1}{12}=0\Rightarrow-x=\frac{1}{12}\Rightarrow x=-\frac{1}{12}\)
15 tháng 10 2021
\(A=139\)
\(\Leftrightarrow720:\left(x-6\right)=40\)
\(\Leftrightarrow x-6=18\)
hay x=24
AH
Akai Haruma
Giáo viên
24 tháng 3 2023
Lời giải:
Áp dụng BĐT $|a|+|b|\geq |a+b|$ ta có:
$A=(|2x-4|+|2x-8|)+|2x-6|=(|2x-4|+|8-2x|)+|2x-6|$
$\geq |2x-4+8-2x|+|2x-6|$
$=4+|2x-6|\geq 4$
Vậy $A_{\min}=4$. Giá trị này đạt tại \(\left\{\begin{matrix}
(2x-4)(8-2x)\geq 0\\
2x-6=0\end{matrix}\right.\Leftrightarrow x=3\)
PT
Với giá trị nào của x thì B = |x − 1| + |x − 2| + |x − 3| + |x − 5| đạt giá trị nhỏ nhất?
1
CM
28 tháng 8 2017
Với mọi x ta có: |x| ≥ x; dấu “=” xảy ra khi x ≥ 0. Do đó:
B = |x − 1| + |x − 2| + |3 − x| + |5 − x|
⇒ B ≥ x – 1 + x – 2 + 3 – x + 5 – x = 5
Dấu ''='' xảy ra khi và chỉ khi
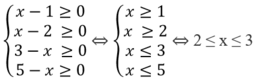
Vậy với 2 ≤ x ≤ 3 thì B đạt giá trị nhỏ nhất là 5.
DT
1
PC
7 tháng 9 2016
Vì \(x\ge0\forall x\in R\)
=) \(x+\frac{3}{4}\ge\frac{3}{4}\forall x\in R\)
Dấu "=" xảy ra khi và chỉ khi : \(x+\frac{3}{4}=0\)
\(\Rightarrow x=-\frac{3}{4}\)
Vậy GTNN của \(A=\left|x+\frac{3}{4}\right|\) = 0 khi và chỉ khi \(x=-\frac{3}{4}\)
CM
21 tháng 4 2018
Ta có:
|x – 3| + |x – 7| = |x – 3| + |7 – x| ≥ |x – 3 + 7 – x| = |4| = 4.
(áp dụng bài 140: |x| + |y| ≥|x + y|)
* Lại có: |x – 5| ≥ 0.
Vậy A = |x – 3| + |x – 5| + |x – 7| ≥ 4 + 0 = 4.
Dấu ''='' xảy ra khi và chỉ khi: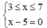 
, tức là x = 5.
Vậy với x = 5 thì A đạt giá trị nhỏ nhất là 4.
PT
3
WR
24 tháng 6 2019
Theo BDDT trị tuyệt đối\(B=\left|x-1\right|+\left|x-2\right|+\left|x-3\right|+\left|x-5\right|=\left(\left|x-1\right|+\left|5-x\right|\right)+\left(\left|x-2\right|+\left|3-x\right|\right)\)\(\ge\left|x-1+5-x\right|+\left|x-2+3-x\right|=5\)
=> Min B=5
Dấu bằng xảy ra khi \(\hept{\begin{cases}\left(x-2\right)\left(3-x\right)\ge0\\\left(x-1\right)\left(5-x\right)\ge0\end{cases}\Leftrightarrow\hept{\begin{cases}2\le x\le3\\1\le x\le5\end{cases}\Leftrightarrow}2\le x\le3}\)
A
24 tháng 6 2019
Ta có :
\(B=|x-1|+|x-2|+|3-x|+|5-x|\)
\(\Rightarrow B\ge x-1+x-2+3-x+5-x=5\)
Dấu ''='' xảy ra khi và chỉ khi
\(x-1\ge0\Leftrightarrow x\ge1\)
\(x-2\ge0\Leftrightarrow x\ge2\)\(3-x\ge0\Leftrightarrow x\le3\)
\(5-x\ge0\Leftrightarrow x\le5\)\(\Leftrightarrow2\le x\le3\)
Vậy với 2 ≤ x ≤ 3 thì B đạt giá trị nhỏ nhất là 5.
\(P=\left(x-1\right)\left(x+2\right)\left(x+3\right)\left(x+6\right)\)
\(P=\left[\left(x-1\right)\left(x+6\right)\right]\left[\left(x+2\right)\left(x+3\right)\right]\)
\(P=\left(x^2+5x-6\right)\left(x^2+5x+6\right)\)
\(P=\left(x^2+5x\right)^2\ge-36\)
\(\Rightarrow GTNN\) của \(P=-36\)
Dấu = sảy ra khi:\(x^2+5x=0\)
.....................\(\Rightarrow x=0\) hoặc \(x=-5\)