Cho hai hàm số bậc nhất
y = (m - 1)x + n - 2
y = (1 - 2m)x + 3 + n
Tìm m để 2 đồ thị hàm số trên là 2 đường thẳng
Trùng nhau
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2 tháng 9 2021
Để hai đường thẳng trùng nhau thì
\(\left\{{}\begin{matrix}m-1=1-2m\\n-2=n+3\left(loại\right)\end{matrix}\right.\)
2 tháng 9 2021
a: Để hai đường thẳng song song thì \(\left\{{}\begin{matrix}m-1=1-2m\\n-2\ne n+3\end{matrix}\right.\Leftrightarrow3m=2\Leftrightarrow m=\dfrac{2}{3}\)
b: Để hai đường thẳng cắt nhau thì \(m-1\ne-2m+1\)
\(\Leftrightarrow3m\ne2\)
hay \(m\ne\dfrac{2}{3}\)
11 tháng 12 2021
\(1,\Leftrightarrow m=2m+1\Leftrightarrow m=-1\\ 2,\Leftrightarrow a=-5\)
T
10 tháng 12 2020
1. Để 2 đồ thị hàm số đã cho là hai đường thẳng song song thì
\(\left\{{}\begin{matrix}m+1=2m+1\\2m\ne3m\end{matrix}\right.\left(ĐK:m\ne-1,-\dfrac{1}{2}\right)\)
Hệ phương trình tương đương với:
\(\left\{{}\begin{matrix}m=0\\m\ne0\end{matrix}\right.\Rightarrow\text{Hệ\:phương\:trình\:vô\:nghiệm}\)
Vậy không tồn tại giả trị m để đồ thị của hai hàm số trên song song.
2. Để giao điểm hai đồ thì nằm trên trục hoành thì y = 0.
\(y=\left(m+1\right)x+2m=0\Rightarrow x=-\dfrac{2m}{m+1}\) (1)
\(y=\left(2m+1\right)x+3m=0\Rightarrow x=-\dfrac{3m}{2m+1}\) (2)
và \(m+1\ne2m+1\Rightarrow m\ne0\) (3)
Từ (1) và (2) và (3) ta tìm được m = 1.
31 tháng 8 2021
a: Để hai đồ thị song song thì \(\left\{{}\begin{matrix}2m-3=m\\n-2\ne3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=3\\n\ne5\end{matrix}\right.\)
31 tháng 8 2021
b: Để hai đồ thị cắt nhau thì \(2m-3\ne m\)
hay \(m\ne3\)
23 tháng 12 2021
a: Để hàm số là hàm số bậc nhất thì 2m-3<>0
hay m<>3/2
b: Để hàm số đồng biến thì 2m-3>0
hay m>3/2
Để hàm số nghịch biến thì 2m-3<0
hay m<3/2
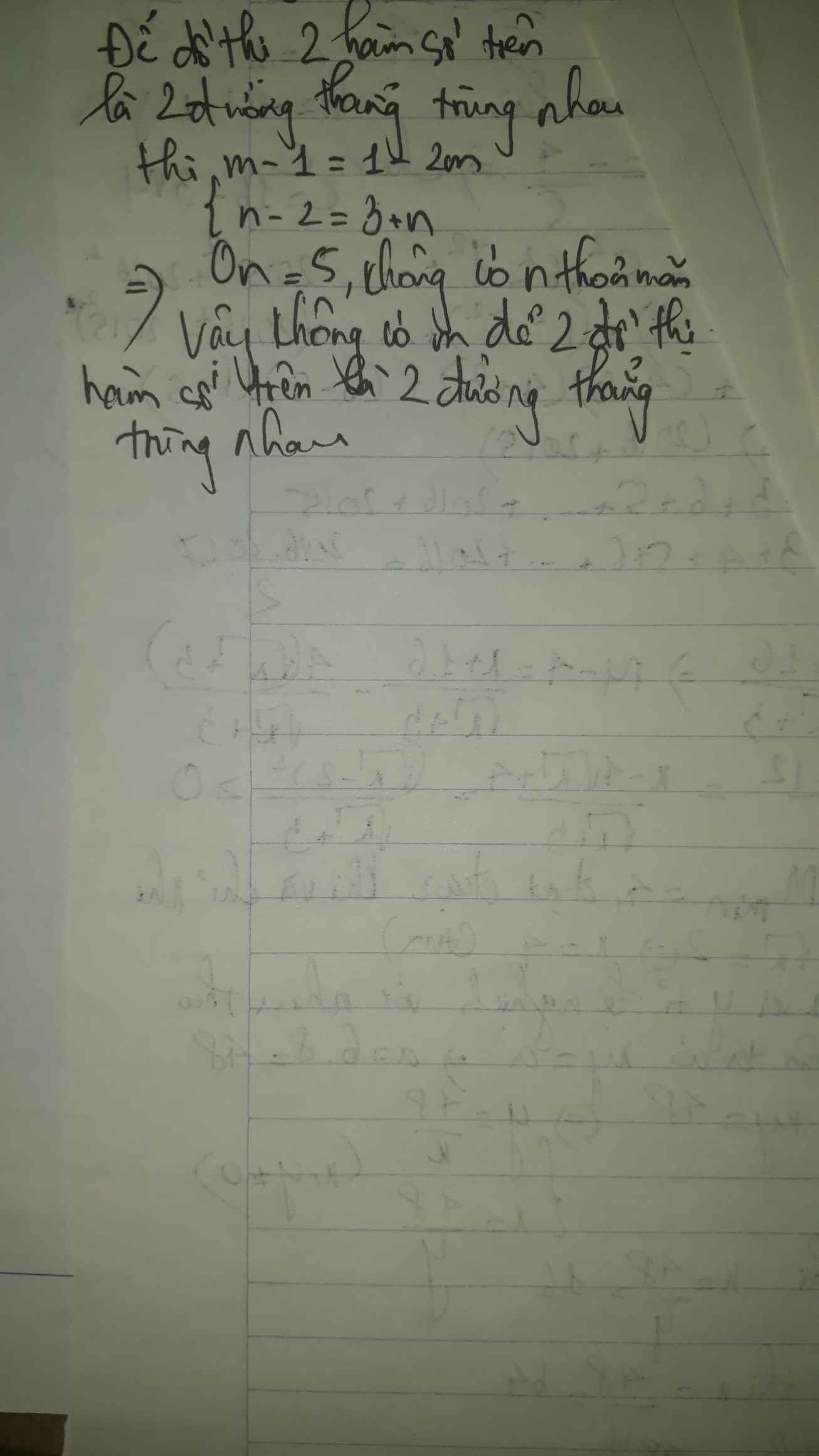
a: Để hai đường thẳng trùng nhau thì \(\left\{{}\begin{matrix}m-1=1-2m\\n-2=n+3\left(loại\right)\end{matrix}\right.\)
Vậy: Không có (m,n) nào để hai đường thẳng trùng nhau