Hai bến A,B của 1 con sông thẳng cách nhau một khoảng AB là 60km. Một cano xuôi dòng từ A đến B mất thời gian là 2 giờ, ngược dòng từ B đến A mất thời gian là 3 giờ. Tính vận tốc cano và vận tốc dòng nước
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tham khảo:
gọi x(km/h) là vận tốc thực của cano (x > 0)
=> vận tốc khi đi xuôi là x + 2(km/h) và vận tốc khi đi ngược là x-2(km/h)
=> thời gian khi đi xuôi là \(\dfrac{80}{x+2}\) và thời gian khi đi ngược là \(\dfrac{80}{x-2}\)
vì thời gian xuôi dòng mất ít hơn thời gian ngược dòng là 1 giờ
nên \(\dfrac{80}{x+2}\) + 1 = \(\dfrac{80}{x-2}\)
<=> \(\dfrac{x+82}{x+2}\)= \(\dfrac{80}{x-2}\)
<=> (x + 82)(x - 2) = 80(x + 2)
<=> x2 - 2x + 82x - 164 = 80x + 160
<=> x2 + 80x - 164 = 80x + 160
<=> x2 = 324
<=> x = 18 và x>0
vậy vận tốc thực của cano là......
Gọi vận tốc của cano là x (km/h; x\(\in\)N*)
Khi đó:
vận tốc của cano khi xuôi dòng là x +2(km/h)
vận tốc của cano khi ngược dòng là:x-2(km/h )
Thời gian khi đi xuôi dòng là: 80/x+2(giờ)
Thời gian khi đi ngược dòng là: 80/x−2(giờ)
Theo đề ra ta có phương trình:
\(\dfrac{80}{x-2}-\dfrac{80}{x+2}=1\) \(\Leftrightarrow80\left(x+2\right)-80\left(x-2\right)=2^2-4\)
\(\Leftrightarrow80x+160-80x+160-x^2=-4\)
\(\Leftrightarrow-x^2=-4-160-160\)
\(\Leftrightarrow-x^2=-360\Leftrightarrow x=60\)
Vậy vận tốc thực của cano là 60km/h

a) gọi van toc cano la v ta co;
30: (v-5) = 1h30p = 3/2
v = 25km/h
b) thoi gian cano di xuoi la;
30:(v+5) = 30/25+5 = 30/30 = 1h

| V(km/h) | t(h) | S(km) | |
| Ca nô xuôi dòng | x4 | 4 | x |
| Ca nô ngược dòng | x5 | 5 | x |
Giải:
Gọi khoảng cách giữa hai bến ca nô là x km(x>0)
Vậy: Vận tốc xuôi dòng của ca nô là x4 (km/h)
Vận tốc ngược dòng của ca nô là x5 (km/h)
Mà vận tốc của dòng nước là 2km/h Nên khi xuôi dòng vận tốc của ca nô nhiều hơn vận tốc khi đi ngược dòng của ca nô là 4km/h
Do đó ta có phương trình: x4−x5=4
⇔5x−4x=4.20⇔x=80(TMĐK)
Vậy khoảng cách giữa hai điểm A và B là 80km

Gọi khoảng cách từ A đến B là x ( km ) ( x>0 )
Vận tốc xuôi dòng là: \(\dfrac{x}{4}\) (h)
Vận tốc ngược dòng là: \(\dfrac{x}{5}\) (h)
Theo đề bài ta có pt:
\(\dfrac{x}{4}-\dfrac{x}{5}=2.2\)
\(\Leftrightarrow\dfrac{5x-4x}{20}=\dfrac{80}{20}\)
\(\Leftrightarrow x=80\left(tm\right)\)
Vậy khoảng cách từ A đến B là 80km
Gọi vận tốc cano khi nước lặng là x km/h với x>2
Vận tốc cano khi xuôi dòng: x+2 (km/h)
Quãng đường cano đi xuôi dòng: \(4\left(x+2\right)\)
Vận tốc cano khi ngược dòng: \(x-2\) (km/h)
Quãng đường cano đi ngược dòng: \(5\left(x-2\right)\) (km/h)
Do độ dài quãng đường xuôi dòng và ngược dòng như nhau nên ta có pt:
\(4\left(x+2\right)=5\left(x-2\right)\)
\(\Leftrightarrow x=18\) (km/h)
Độ dài AB: \(4\left(18+2\right)=80\left(km\right)\)

a)
Ta ký hiệu canô là (1), nước là (2), bờ sông là (3)
Áp dụng công thức cộng vận tốc: 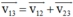 (0,25 đ)
(0,25 đ)
Khi canô xuôi dòng: 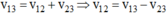 (0,50 đ)
(0,50 đ)
Mà 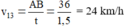 (0,25đ)
(0,25đ)
Vậy vận tốc của canô đối với nước: v 12 = 24 – 6 = 18 km/h (0,25đ)
b) Khi ca nô đi ngược dòng:
v 13 = v 12 - v 23 (0,25đ)
= 18 - 6 = 12 km/h (0,25đ)
Vậy thời gian ngược dòng của canô: 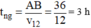 (0,25đ)
(0,25đ)

a) Gọi: (0,25 điểm)
(1): canô (2): nước (3): bờ sông
Áp dụng công thức cộng vận tốc: 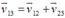 (0,25 điểm)
(0,25 điểm)
Khi canô xuôi dòng:
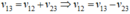 (0,25 điểm)
(0,25 điểm)
Mà 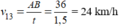 (0,25 điểm)
(0,25 điểm)
Vậy vận tốc của canô đối với nước: v 12 = 24 – 6 = 18 km/h (0,25 điểm)
b) khi ca nô đi ngược dòng: v 13 = v 12 - v 23 (0,25 điểm)
= 18 - 6 = 12 km/h (0,25 điểm)
Vậy thời gian ngược dòng của canô: 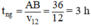 (0,25 điểm)
(0,25 điểm)
Vx là vận tốc xuôi,Vcn là vậ tốc ca nô
Vn vận tốc nước
Vng là vận tốc ngược:
=> Vx=S/tx=60/2=30
Vng=S/tng=60/3=20
mà Vx=Vcn+Vn
Vng=Vcn-Vn
=> Vcn=Vx+Vng/2=25
Vn=30-25=5