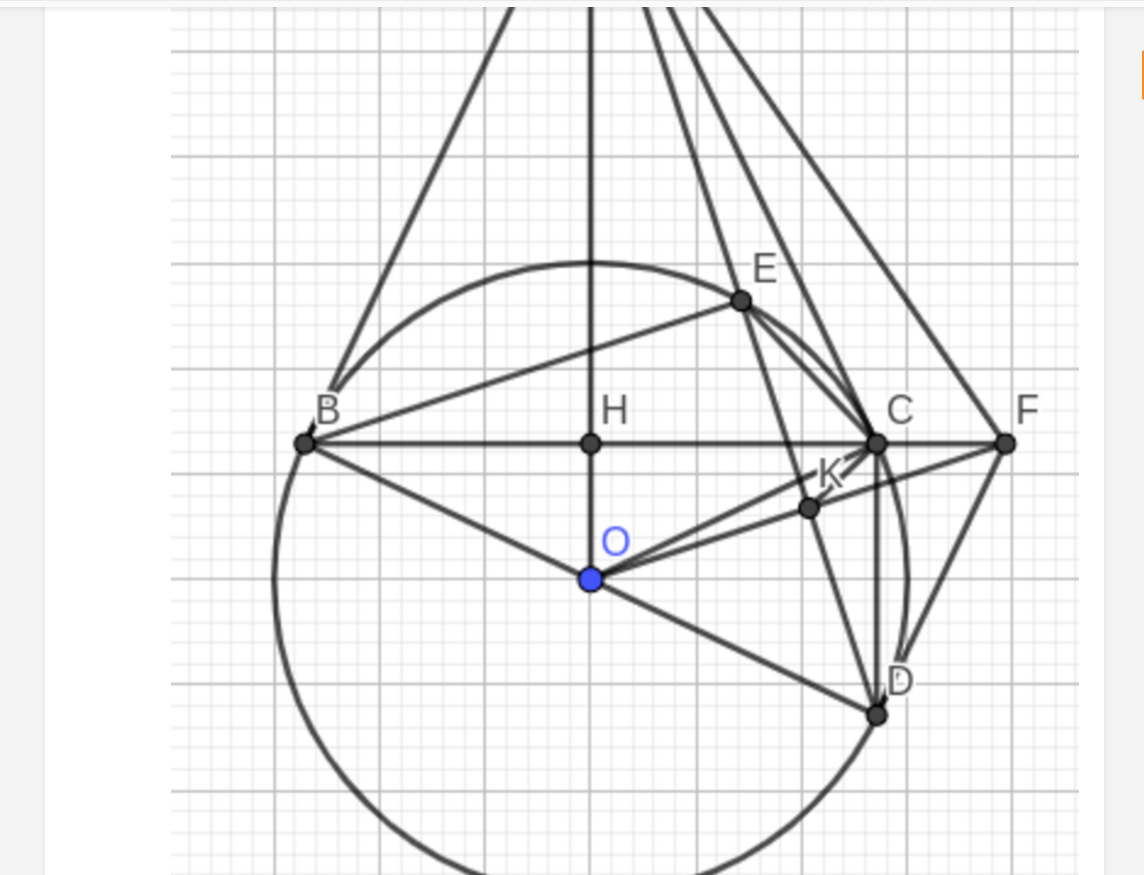
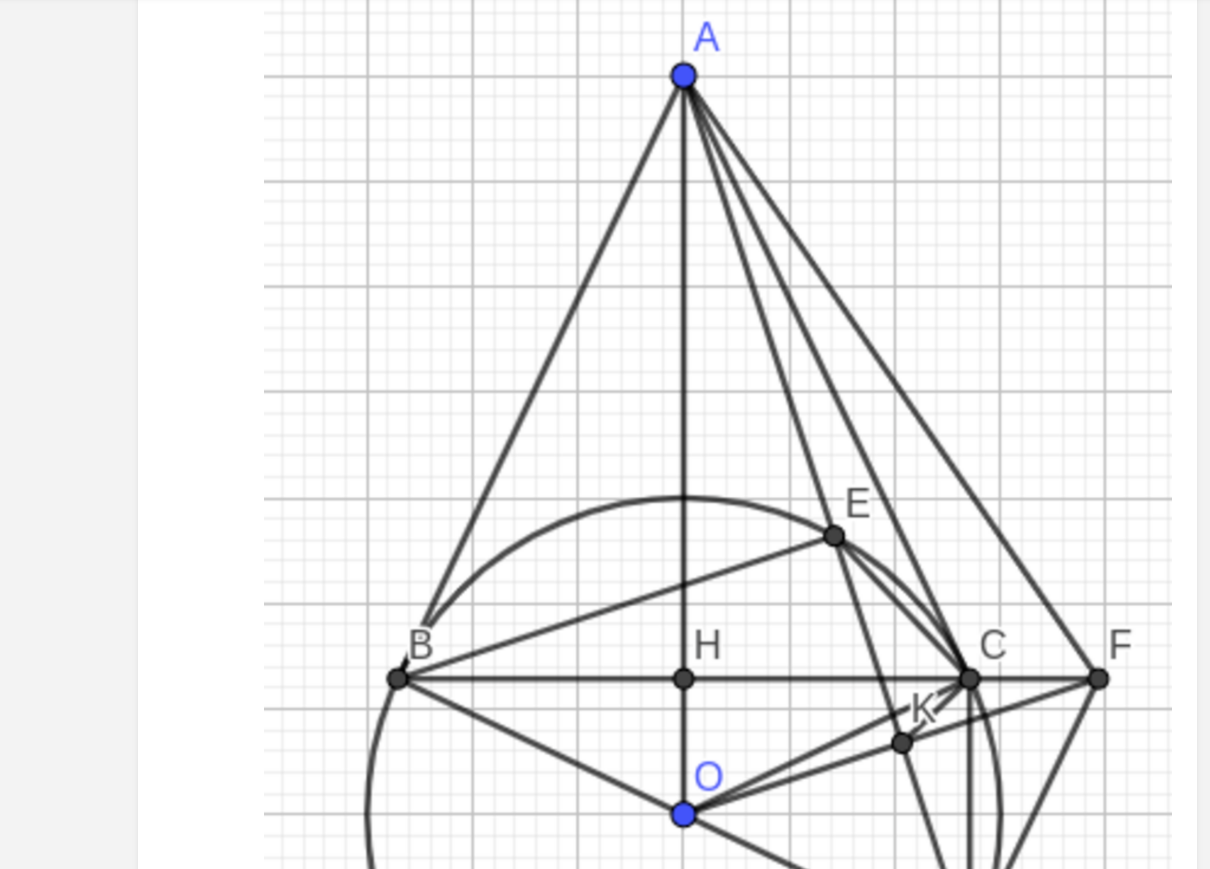
Bài 1: Cho hai đường tròn (O) và (O') tiếp xúc ngoài tại B. Vẽ tiếp tuyến chung ngoài AC với A thuộc (O), C thuộc (O'). Tiếp tuyến chung trong tại B cắt AC tại M, MO cắt AB ở K, MO' cắt BC ở H.
a) Chứng minh tam giác ABC vuông.
b) Tính số do góc OMO'
c) Tính độ dài AC biết OB= 5cm, O'B = 3,2cm.
d) Tứ giác BKMH là hình gì? Vì sao?
e) Chứng minh dẳng thức MK.MO = MH.MO'
f) Chứng minh OO' là tiếp tuyến của đường tròn có đường kính AC.
g) Chứng minh AC là tiếp tuyến của đường tròn có đường kính OO'.
Bài 2: Cho đoạnthẳng AB, điểm C nằm giữa A và B. Vẽ về một phía của AB hai nửa đường tròn tâm O và P có đường kính theo thứ tự là AB và AC. Đường vuông góc với AB tại C cắt nửa đường tròn (P) tại M. Gọi N là chân đường vuôn góc kẻ từ C đến DB. Gọi Q là tâm nửa đường tròn ngoại tiếp tam giác CNB.
a) Xác định vị trí tương đối giữa các đường tròn (O) và (P) ; (O) và(Q) ; (P) và (Q).
b) Tứ giác DMCN là hình gì? Vì sao?
c) Chứng minh hệ thức DM.DA = DN.DB
d) Chứng minh MN là tiếp tuyến chung của các nửa đường tròn (P) và (Q)
e) Điểm C ở vị trí nào trên AB thì MN có độ dài lớn nhất.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan

30 tháng 12 2021
a: Xét (O) có
AB là tiếp tuyến
AC là tiếp tuyến
Do đó: AB=AC
hay A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
nên O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OA⊥BC

DT
23 tháng 2 2022
giải b2:
a, MPHQ là hình chữ nhật => MH = PQ
b, Sử dụng hệ thức lượng trong tam giác vuông chứng minh được MP.MA = MQ.MB => ∆MPQ: ∆MBA
c,\(\widehat{PMH}=\widehat{MBH}\Rightarrow\widehat{PQH}=\widehat{O_2QP}\) => PQ là tiếp tuyến của \(\left(O_2\right)\)
Tương tự PQ cũng là tiếp tuyến \(\left(O_1\right)\)