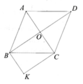
Cho hình thoi ABCD. Gọi O là giao điểm hai đường chéo. Qua D kẻ đường thẳng d song song với AC. Qua C kẻ đường thẳng d' song song DB; d và d' cắt nhau tại E.
a. ODEC là hình chữ nhật
b. BC=OE
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
29 tháng 11 2019
Quá nhiều cách để chứng minh.
a. CE //BD
BE // DC ( vì DC // AB )
=> DCEB là hình bình hành
=> CE = BD
Mà BD =AC ( vì ABCD là hv)
=> CE = AC (1)
BD vuông AC ( vì ABCD là hình vuông )
mà CE // BD
=> CE vuông AC (2)
Từ (1); (2) => Tam giác ACE là tam giác vuông cân.
b) F đối xứng với AB qua O
=> AB là đường trung trực của OF
=> BF = BO và AO = AF
Mà OA = OB ( ABCD là hình bình hành vs O là giao 2 đường chéo )
=> BF = BO = AO = AF.
=> AOBF là hình thoi
Mặt khác ^AOB = 90^o
=> AOBF là hình vuông
c. APCQ là hình thoi
=>đường thẳng PQ là đường trung trực của đoạn AC (3)
Mặt khác ABCD là hình vuông => đường thẳng BD là đường trung trực của đoạn AC(4)
Từ (3); (4) => Đường thẳng PQ trùng đường thẳng BD => P; D; B; Q thẳng hàng.
27 tháng 12 2022
THAM KHẢO
a) BK//OC, CK//OB.
Mà OB ^OC Þ OBKC là hình chữ nhật.
b)ABCD là hình thoi nên AB = BC. OBKC là hình chữ nhật nên KO =BC.
Þ KO = BC Þ ĐPCM.
c) nếu OBKC là hình vuông thì OB = OC Þ BD = AC. Vậy ABCD là hình vuông
9 tháng 11 2016
a/ Xét tứ giác ABCD ta có:
BK // AC
mà O thuộc AC nên BK // OC
mà O thuộc BD nên KC // BO
=> tứ giác OBKC là hbh
mặt khác ta có:
BD vuông góc với AC tại O ( vì ABCD là hình thoi)
=> góc O= 90 độ
nên hbh OBKC là hcn
b/ Ta có AB=BC (vì tứ giác ABCD là hình thoi)
Mặt khác BC=OK (vì OBKC là hcn )
=> AB = OK
Lời giải:
a)
Vì $ABCD$ là hình thoi nên hai đường chéo $AC$ và $BD$ vuông góc với nhau
\(\Rightarrow \angle DOC=90^0\)
Ta có:
\(\left\{\begin{matrix} DE\parallel AC\\ AC\perp BD\end{matrix}\right.\Rightarrow DE\perp BD\Rightarrow \angle EDB=90^0\)
\(\left\{\begin{matrix} CE\parallel BD\\ BD\perp AC\end{matrix}\right.\Rightarrow CE\perp AC\Rightarrow \angle OCE=90^0\)
Xét tứ giác $ODEC$ có 3 góc đều là góc vuông nên là hình chữ nhật (đpcm)
b) Vì $ODEC$ là hình chữ nhật nên hai đường chéo $CD$ và $OE$ bằng nhau (\(OE=CD)\)
Mà $ABCD$ là hình thoi nên $BC=CD$
\(\Rightarrow OE=BC\) (đpcm)
E cảm ơn cô nhiều ạ