Giúp mik giải bài 2 câu d nhanh với ạ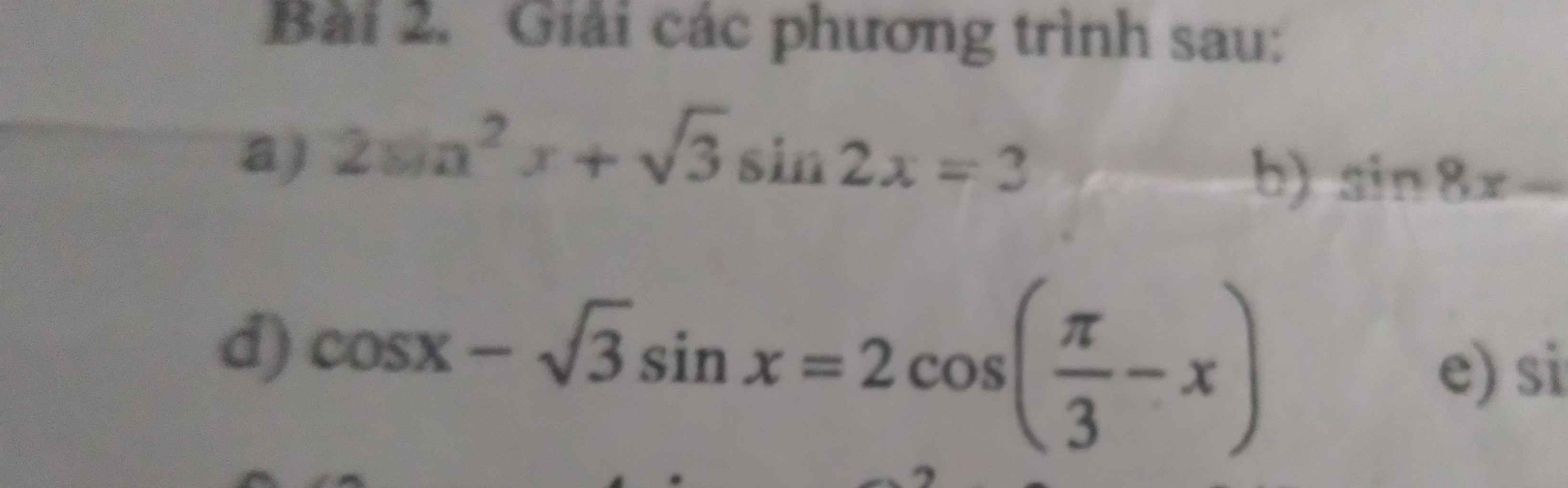
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 8 2022
3. She said I should ask a lawyer.
4. Mrs Linh asked me to give Tuan this book.
5 tháng 3 2022
Câu 3:
a: \(BD=\sqrt{BC^2-DC^2}=4\left(cm\right)\)
b: \(\widehat{A}=180^0-2\cdot70^0=40^0< \widehat{B}\)
nên BC<AC=AB
c: Xét ΔEBC vuông tại E và ΔDCB vuông tại D có
BC chung
\(\widehat{EBC}=\widehat{DCB}\)
Do đó:ΔEBC=ΔDCB
d: Xét ΔOBC có \(\widehat{OBC}=\widehat{OCB}\)
nên ΔOBC cân tại O
21 tháng 9 2021
\(b,B=\dfrac{\sqrt{x}+2}{\sqrt{x}-3}+\dfrac{\sqrt{x}-8}{x-5\sqrt{x}+6}\left(x\ge0;x\ne4;x\ne9\right)\\ B=\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)+\sqrt{x}-8}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\\ B=\dfrac{x-4+\sqrt{x}-8}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}-4\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{\sqrt{x}-4}{\sqrt{x}-2}\)
\(c,B< A\Leftrightarrow\dfrac{\sqrt{x}-4}{\sqrt{x}-2}< \dfrac{\sqrt{x}+1}{\sqrt{x}-2}\Leftrightarrow\dfrac{\sqrt{x}-4}{\sqrt{x}-2}-\dfrac{\sqrt{x}+1}{\sqrt{x}-2}< 0\\ \Leftrightarrow\dfrac{-5}{\sqrt{x}-2}< 0\Leftrightarrow\sqrt{x}-2>0\left(-5< 0\right)\\ \Leftrightarrow x>4\\ d,P=\dfrac{B}{A}=\dfrac{\sqrt{x}-4}{\sqrt{x}-2}:\dfrac{\sqrt{x}+1}{\sqrt{x}-2}=\dfrac{\sqrt{x}-4}{\sqrt{x}+1}=1-\dfrac{5}{\sqrt{x}+1}\in Z\\ \Leftrightarrow5⋮\sqrt{x}+1\Leftrightarrow\sqrt{x}+1\inƯ\left(5\right)=\left\{-5;-1;1;5\right\}\\ \Leftrightarrow\sqrt{x}\in\left\{-6;-2;0;4\right\}\\ \Leftrightarrow x\in\left\{0;16\right\}\left(\sqrt{x}\ge0\right)\)
\(e,P=1-\dfrac{5}{\sqrt{x}+1}\)
Ta có \(\sqrt{x}+1\ge1,\forall x\Leftrightarrow\dfrac{5}{\sqrt{x}+1}\ge5\Leftrightarrow1-\dfrac{5}{\sqrt{x}+1}\le-4\)
\(P_{max}=-4\Leftrightarrow x=0\)
HP
20 tháng 9 2021
a. \(\sqrt{x^2-2x+4}=2x-2\)
<=> x2 - 2x + 4 = (2x - 2)2
<=> x2 - 2x + 4 = 4x2 - 8x + 4
<=> 4x2 - x2 - 8x + 2x + 4 - 4 = 0
<=> 3x2 - 6x = 0
<=> 3x(x - 2) = 0
<=> \(\left[{}\begin{matrix}3x=0\\x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
b. \(\sqrt{x^2-2x}=\sqrt{2-3x}\)
<=> x2 - 2x = 2 - 3x
<=> x2 + 3x - 2x - 2 = 0
<=> x2 + x - 2 = 0
<=> x2 + 2x - x - 2 = 0
<=> x(x + 2) - (x + 2) = 0
<=> (x - 1)(x + 2) = 0
<=> \(\left[{}\begin{matrix}x-1=0\\x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\)
c. (Tương tự câu a)
A
2
3 tháng 9 2021
a) \(A=\sqrt{1-x}+\sqrt{1+x}\)
\(\Rightarrow A^2=1-x+1+x+2\sqrt{\left(1-x\right)\left(1+x\right)}=2+2\sqrt{1-x^2}\)
Do \(-x^2\le0\Rightarrow1-x^2\le1\Rightarrow A^2=2+2\sqrt{1-x^2}\le2+2=4\)
\(\Rightarrow A\le2\)
\(maxA=2\Leftrightarrow x=0\)
Áp dụng bất đẳng thức: \(\sqrt{x}+\sqrt{y}\ge\sqrt{x+y}\)(với \(x,y\ge0\))
\(\Leftrightarrow\left(\sqrt{x}+\sqrt{y}\right)^2\ge x+y\)
\(\Leftrightarrow x+y+2\sqrt{xy}\ge x+y\Leftrightarrow2\sqrt{xy}\ge0\left(đúng\right)\)
\(A=\sqrt{1-x}+\sqrt{1+x}\ge\sqrt{1-x+1+x}=\sqrt{2}\)
\(maxA=\sqrt{2}\Leftrightarrow\)\(\left[{}\begin{matrix}1-x=0\\1+x=0\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)
a, \(2sin^2x+\sqrt{3}sin2x=3\)
\(\Leftrightarrow-\left(1-2sin^2x\right)+\sqrt{3}sin2x=2\)
\(\Leftrightarrow\sqrt{3}sin2x-cos2x=2\)
\(\Leftrightarrow\dfrac{\sqrt{3}}{2}sin2x-\dfrac{1}{2}cos2x=1\)
\(\Leftrightarrow sin\left(2x-\dfrac{\pi}{6}\right)=1\)
\(\Leftrightarrow2x-\dfrac{\pi}{6}=\dfrac{\pi}{2}+k2\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{3}+k\pi\)
d, \(cosx-\sqrt{3}sinx=2cos\left(\dfrac{\pi}{3}-x\right)\)
\(\Leftrightarrow\dfrac{1}{2}cosx-\dfrac{\sqrt{3}}{2}sinx=cos\left(\dfrac{\pi}{3}-x\right)\)
\(\Leftrightarrow cos\left(x+\dfrac{\pi}{3}\right)=cos\left(\dfrac{\pi}{3}-x\right)\)
\(\Leftrightarrow-2sin\dfrac{\pi}{3}.sinx=0\)
\(\Leftrightarrow sinx=0\)
\(\Leftrightarrow x=k\pi\)