Cho hình chóp S.ABCD.Gọi O là giao điểm của AC và BD.Lấy M,N,P lần lượt là các điểm trên SA,SB,SC.tìm giao điểm I của SO với mặt phẳng (MNP). Tìm giao điểm của đường thẳng MC và mặt phẳng (SBD)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
14 tháng 10 2017
Chọn đáp án D
Ta có
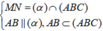
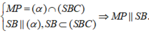
Khi đó 
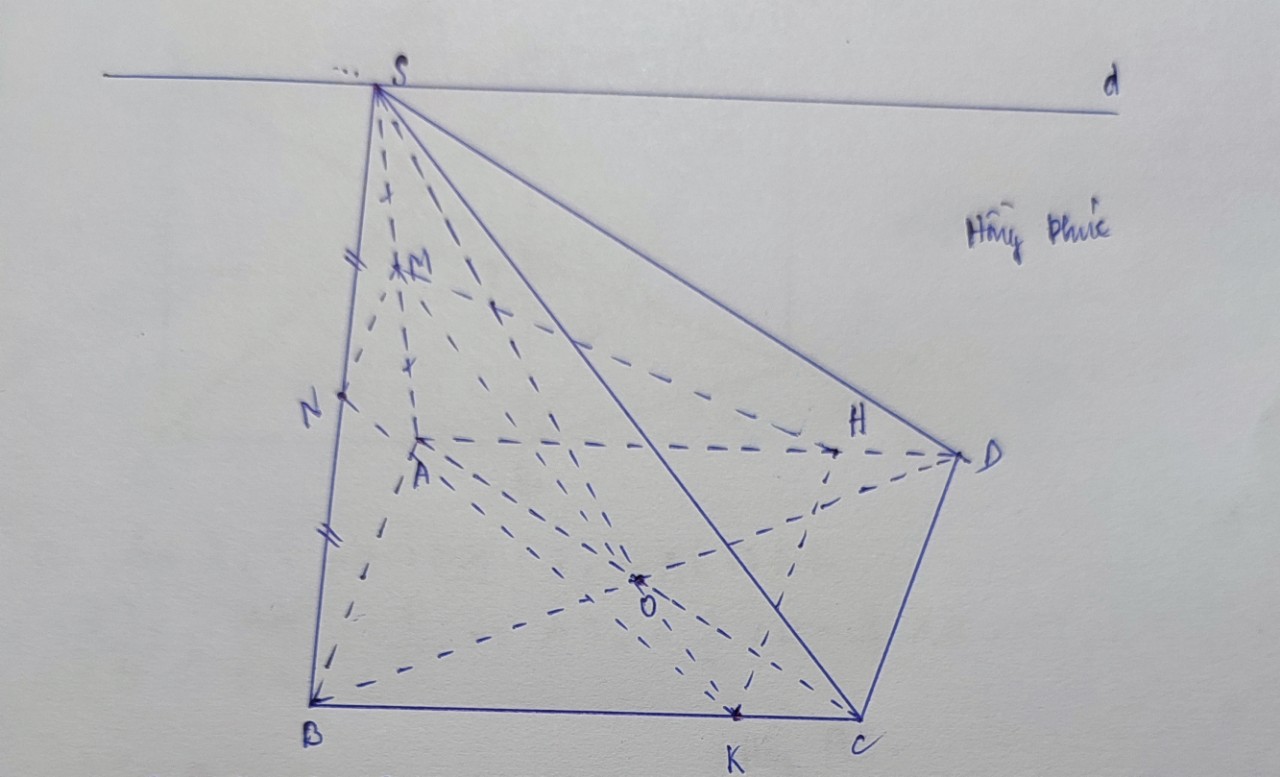
Gọi I là trung điểm của AB.
Ta có SA=SB=AB=CA=CB=a nên tam giác SAB và tam giác ABC đều cạnh a.
Khi đó A B ⊥ S I , A B ⊥ C I và S I = C I = a 3 a
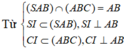
Mặt khác S I = C I = S C = a 3 2 nên ∆ S I C đều
Vậy góc giữa hai mặt phẳng (MNP) và (ABC) bằng 60 0
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 12 2021
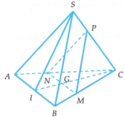
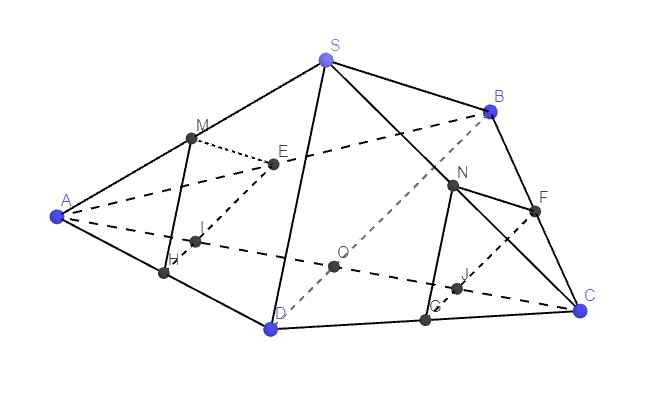
a. Qua M kẻ đường thẳng song song SB cắt AB tại E
Qua M kẻ đường thẳng song song SD cắt AD tại H
\(\Rightarrow\Delta MEH\) là thiết diện của mp qua M và song song (SBD)
Qua N kẻ đường thẳng song song SB cắt BC tại F
Qua N kẻ đường thẳng song song SD cắt CD tại G
\(\Rightarrow NFG\) là thiết diện của mp qua N và song song (SBD)
b. Gọi O là giao điểm AC và BD
Do M là trung điểm SA, \(ME||SB\Rightarrow ME\) là đường trung bình tam giác SAB
\(\Rightarrow\) E là trung điểm AB
Hoàn toàn tương tự, ta có F là trung điểm BC, G là trung điểm CD, H là trung điểm AD
\(\Rightarrow EH\) là đường trung bình tam giác ABD, FG là đtb tam giác BCD
\(\Rightarrow I\) là trung điểm AO, J là trung điểm CO
\(\Rightarrow\left\{{}\begin{matrix}OI=\dfrac{1}{2}OA\\OJ=\dfrac{1}{2}OC\end{matrix}\right.\) \(\Rightarrow OI+OJ=\dfrac{1}{2}\left(OA+OC\right)\Rightarrow IJ=\dfrac{1}{2}AC\)
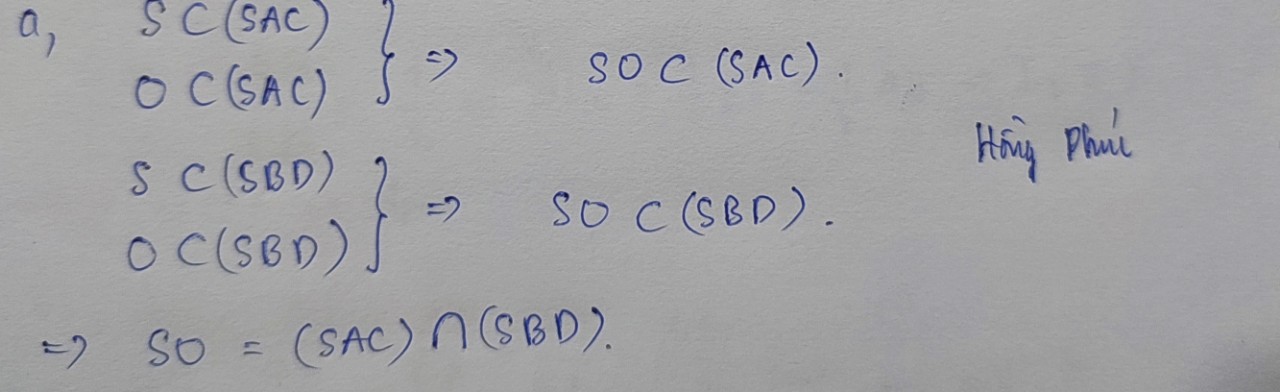
a) xét tam giác SAC
gọi \(SO\cap MP=\left\{E\right\}\)\(\left(SO,MP\subset\left(SAC\right)\right)\)
ta có \(MP\subset\left(MNP\right)\)
vậy \(SO\cap\left(MNP\right)=\left\{E\right\}\)