Cho đường tròn (O) .Từ một điểm M ở ngoài (O),Vẽ hai tiếp tuyến ME và MF sao cho góc EMO=30 độ .Biết chu vi tam giác MEF là 30 cm .Tính độ dài dây EF.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
15 tháng 6 2017
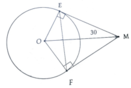
a, Chứng minh: E M F ^ = 60 0 => ΔMEF đều => EF = 10cm
b, Tìm được: S M E F = 25 3 cm
26 tháng 1 2023
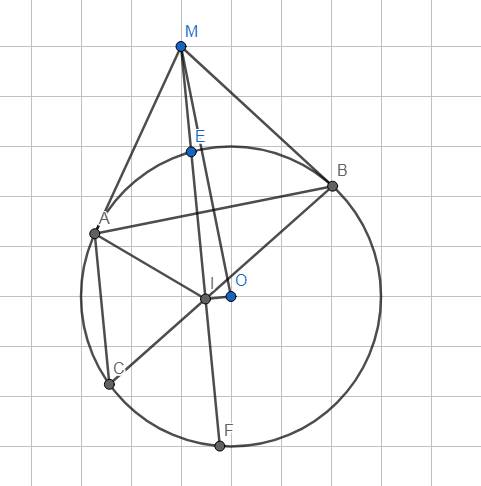
*Mấu chốt bài này là c/m 5 điểm M,A,I,O,B nằm trên cùng 1 đg tròn.
- Ta có: △OAM vuông tại A, △OBM vuông tại B.
\(\Rightarrow\)△OAM, △OBM nội tiếp đường tròn đường kính OM.
\(\Rightarrow\)AMBO nội tiếp đường tròn đường kính OM (1).
- Ta có AC//EF \(\Rightarrow\widehat{ACB}=\widehat{MIB}\) (2 góc so le trong).
- Trong (O) có:
\(\widehat{ACB}\) là góc nội tiếp chắn cung AB.
\(\widehat{MAB}\) là góc tạo bởi tia tiếp tuyến MA và dây cung AB.
\(\Rightarrow\widehat{ACB}=\widehat{MAB}\)
\(\Rightarrow\widehat{MAB}=\widehat{MIB}\). Do đó AIBM nội tiếp (2). (2 góc cùng nhìn 1 cạnh bằng nhau).
\(\left(1\right),\left(2\right)\Rightarrow\)A,M,B,O,I cùng nằm trên đường tròn đường kính OM.
\(\Rightarrow\)△OIM nội tiếp đường tròn đường kính OM.
\(\Rightarrow\)△OIM vuông tại I nên OI vuông góc với EF tại I.
Trong (O): EF là dây cung, OI là 1 phần đường kính, \(OI\perp EF\) tại I..
\(\Rightarrow\)I là trung điểm EF (đpcm).
