Cho tam giác ABC vuông tại A, đường cao AH. Biết BH= 4cm, CH= 9cm. Gọi D,E lần lượt là hình chiếu vuông góc của H trên cạch AB và AC
a) Tứ giác ADHE là hình gì, tại sao? Tính DE
b) Các đường thẳng vuông góc DE tại D và E lần lượt cắt BC tại M và N. C/m MN=1/2BC
c) Tính diện tích tứ giác DEMN
d) C/m AD.AB=AE.AC

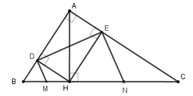
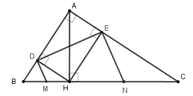
a: Xét tứ giác ADHE có
\(\widehat{EAD}=\widehat{ADH}=\widehat{AEH}=90^0\)
Do đó: ADHE là hình chữ nhật
a: Xét tứ giác ADHE có góc ADH=góc AEH=góc EAD=90 độ
nên ADHE là hình chữ nhật
=>DE=AH=6cm
b: Gọi O là giao của AH và DE
=>O là trung điểm chung của AH và DE
mà AH=DE
nên OA=OH=OD=OE
Ta có: góc OHD+góc MHD=90 độ
góc ODH+góc MDH=90 độ
mà góc OHD=góc ODH
nên góc MHD=góc MDH
=>ΔMHD cân tại M và góc MDB=góc MBD
=>ΔMBD cân tại M
=>MH=MB
=>M là trung điểm của HB
Cm tương tự, ta được N là trung điểm của HC
=>MN=1/2BC
d: \(AD\cdot AB=AH^2\)
\(AE\cdot AC=AH^2\)
Do đó: \(AD\cdot AB=AE\cdot AC\)