Cho hình chữ nhật ABCD ( AD < CD ) có O là giao điểm của hai đường chéo. Trên tia đối của tia CD lấy điểm E sao cho CE = CD. Gọi F là hình chiếu của D trên BE ; I là giao điểm của AB và CF ; K là giao điểm của AF và BC. CMR 3 điểm O, K, I thẳng hàng.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
9 tháng 5 2020
Xét tứ giác CDNB có \(\widehat{DNB}+\widehat{BCD}=90^o+90^o=180^o\) nên là tứ giác nội tiếp ( 1 )
Xét tứ giác ANBD có \(\widehat{DAB}=\widehat{DNB}=90^o\)nên là tứ giác nội tiếp ( 2 )
Từ ( 1 ) và ( 2 ) suy ra 5 điểm A,N,B,C,D cùng thuộc 1 đường tròn
suy ra tứ giác ANCD nội tiếp đường tròn
CM
12 tháng 4 2018
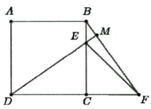
Chứng minh được:
C B F ^ + B E M ^ = M D F ^ + D E C ^ = 90 0
=> B M D ^ = 90 0 nên M thuộc đường tròn đường kính BD. Mà E Î BC nên quỹ tích của điểm M là là cung B C ⏜ của đường tròn đường kính BD
LD
20 tháng 12 2017
e) Chứng minh HI, ST, KF đồng quy.
Gọi O là giao điểm của EI và HK.
Xét tứ giác HIKE ta có:
góc IHE = 900 (HI _|_ EB tại H)
góc IKE = 900 (KI _|_ EC tại K)
góc HEK = 900 (tứ giác ABEC là hình chữ nhật)
=> tứ giác HIKE là hình chữ nhật (tứ giác có 3 góc vuông)
=> góc HIK = 900
=> KI _|_ HI tại I
Xét hình chữ nhật HIKE ta có:
2 đường chéo EI và HK cắt nhau tại O (cách vẽ)
=> O là trung điểm của EI và O là trung điểm của HK
Xét tam giác FEI vuông tại F ta có:
FO là đường trung tuyến ứng với cạnh huyền EI (O là trung điểm của EI)
=> FO = 1/2 EI
Mà EI = HK (tứ giác HIKE là hình chữ nhật)
Nên FO = 1/2 Hk
Xét tam giác FHK ta có:
FO là đường trung tuyến (O là trung điểm của HK)
FO = 1/2 HK (cmt)
=> tam giác FHK vuông tại F
=> HF _|_ FK tại F
Xét tam giác SHK ta có:
ST là đường cao (ST _|_ HK tại T)
HI là đường cao (HI _|_ KI tại I)
KF là đường cao (KF _|_ HF tại F)
=> HI, ST, KF đồng quy tại một điểm (đpcm)
