Cho tứ giác ABCD có 2 đường chéo cắt nhau tại D tạo thành góc nhọn AOD. Chứng minh: Diện tích tứ giác ABCD bằng một nửa AC.BD.sin góc AOD.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Qua 4 đỉnh A,B,C,D của tứ giác ABCD đã cho, dựng các đường thẳng song song với 2 đường chéo AC,BD. Chúng cắt nhau tại 4 điểm M,N,P,Q. Khi đó ta có tứ giác MNPQ,AOBM,AODN,DOCP,BOCQ là các hình bình hành.
Suy ra MQ = NP = AC = 5,3 (cm), MN = PQ = BD = 4 (cm)
Đồng thời ^MNP = ^MQP = ^AOD = 700 (Các góc có 2 cạnh tương ứng song song)
Ta cũng có SAOD = SAND = SAODN/2. Từ đó SABCD = SMNPQ/2 = SMQP = SMNP
Xét \(\Delta\)MNP: MN = 4, NP = 5,3, ^MNP = 700
Có SMNP = 1/2.MN.NP.Sin^MNP = 4.5,3.Sin700 \(\approx\)19,9 (cm2) => SABCD\(\approx\)19.9 (cm2)
Kết luận: ...

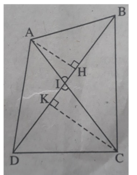
Giả sử hai đường chéo AC, BD cắt nhau tại I, ∠ (AIB) = α là góc nhọn (xem h.bs.9)
Kẻ đường cao AH của tam giác ABD và đường cao CK của tam giác CBD.
Ta có: AH = AI.sin α , CK = CI.sin α
Diện tích tam giác ABD là S A B D = 1/2 BD.AH.
Diện tích tam giác CBD là S C B D = 1/2 BD.CK.
Từ đó diện tích S của tứ giác ABCD là:
S = S A B D + S C B D = 1/2BD.(AH + CK)
= 1/2 BD.(AI + CI)sin α = 1/2BD.AC.sin α

b) Xét ΔFDC có
A\(\in\)FD(gt)
B\(\in\)FC(gt)
AB//CD(gt)
Do đó: \(\dfrac{FA}{AD}=\dfrac{FB}{BC}\)(Định lí Ta lét)
\(\Leftrightarrow\dfrac{FA}{FB}=\dfrac{AD}{BC}=1\)
hay FA=FB
Ta có: FA+AD=FD(A nằm giữa F và D)
FB+BC=FC(B nằm giữa F và C)
mà FA=FB(cmt)
và AD=BC(ABCD là hình thang cân)
nên FD=FC
Ta có: FA=FB(cmt)
FD=FC(cmt)
Do đó: \(FA\cdot FD=FB\cdot FC\)(đpcm)
a) Ta có: ABCD là tứ giác nội tiếp(gt)
nên \(\widehat{A}+\widehat{C}=180^0\)(hai góc đối)(1)
Ta có: ABCD là hình thang(AB//CD)
nên \(\widehat{A}+\widehat{D}=180^0\)(hai góc trong cùng phía)(2)
Từ (1) và (2) suy ra \(\widehat{C}=\widehat{D}\)
Hình thang ABCD(AB//CD) có \(\widehat{C}=\widehat{D}\)(cmt)
nên ABCD là hình thang cân(Dấu hiệu nhận biết hình thang cân)

Có hình vẽ :
Dễ thấy SABCD = \(\frac{1}{2}\left(AH+CK\right).BD\)
mà lại có \(AH=AO.sin\alpha\) ; \(CK=OC.sin\alpha\)
=> SABCD = \(\frac{1}{2}\sin\alpha.AC.BD\)
Khi 2 đường chéo vuông góc với nhau thì
\(H\equiv O\equiv K\Rightarrow AH=AO=CK\)
hay \(sin\alpha=1\)
Khi đó \(S_{ABCD}=\frac{1}{2}mn\)(đpcm)