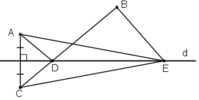
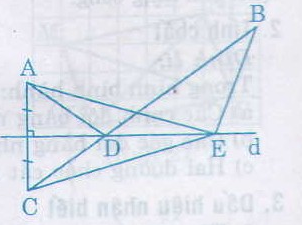
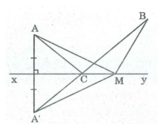
a, Cho hai điểm A,B thuộc cùng một nửa mặt phẳng có bờ là đường thẳng d.Gọi C là điểm đối xứng với A qua d.Gọi D là giao điểm của đường thẳng d và đoạn thẳng BC .Gọi E là điểm bất kì của đường thẳng d.Chứng minh rằng AD+DB<AE+EB
b, Bạn Tú đâng ở vị trí A,cần đến bờ sông d lấy nước rồi đi đến vị trí B.Con sông ngắn nhất mà bạn tú nên đi là con đường nào?





hướng dẫn kể lại những kỉ niệm với con vật nuôi mà em yêu quý