Ai thong minh do trang 114 sach bai tap toan 7. Bai tap48,49
Help me! Can gap
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CD
0
TA
3
31 tháng 8 2015
a) 14 . 50 = (14 : 2)(50 . 2) = 7 . 100 = 700;
16 . 25 = (16 : 4)(25 . 4) = 4 . 100 = 400.
b) 2100 : 50 = (2100 . 2) : (50 . 2) = 4200 : 100 = 42;
1400 : 25 = (1400 . 4) : (25 . 4) = 5600 : 100 = 56.
c) 132 : 12 = (120 + 12) : 12 = 120 : 12 + 12 : 12 = 10 + 1 = 11;
96 : 8 = (80 + 16) : 8 = 80 : 8 + 16 : 8 = 10 + 2 = 12.
18 tháng 6 2016
Các thông tin cần biết khi tham gia Giúp tôi giải toán
"Giúp tôi giải toán" trên Online Math đã trở thành một diễn đàn hết sức sôi động cho các bạn học sinh, các thầy cô giáo và các bậc phụ huynh từ mọi miền đất nước. Ở đây các bạn có thể chia sẻ các bài toán khó, lời giải hay và giúp nhau cùng tiến bộ. Để diễn đàn này ngày càng hữu ích, các bạn lưu ý các thông tin sau đây:
I. Nội qui tham gia "Giúp tôi giải toán"
1. Không đưa câu hỏi linh tinh lên diễn đàn, chỉ đưa các bài mà mình không giải được hoặc các bài toán hay lên diễn đàn;
2. Không trả lời linh tinh, không phù hợp với nội dung câu hỏi trên diễn đàn.
3. Không "Đúng" vào các câu trả lời linh tinh nhằm gian lận điểm hỏi đáp.
Các bạn vi phạm 3 điều trên sẽ bị giáo viên của Online Math trừ hết điểm hỏi đáp, có thể bị khóa tài khoản hoặc bị cấm vĩnh viễn không đăng nhập vào trang web.
II. Cách nhận biết câu trả lời đúng
Trên diễn đàn có thể có rất nhiều bạn tham gia giải toán. Vậy câu trả lời nào là đúng và tin cậy được? Các bạn có thể nhận biết các câu trả lời đúng thông qua 6 cách sau đây:
1. Lời giải rõ ràng, hợp lý (vì nghĩ ra lời giải có thể khó nhưng rất dễ để nhận biết một lời giải có là hợp lý hay không. Chúng ta sẽ học được nhiều bài học từ các lời giải hay và hợp lý, kể cả các lời giải đó không đúng.)
2. Lời giải từ các giáo viên của Online Math có thể tin cậy được (chú ý: dấu hiệu để nhận biết Giáo viên của Online Math là các thành viên có gắn chứ "Quản lý" ở ngay sau tên thành viên.)
3. Lời giải có số bạn chọn "Đúng" càng nhiều thì càng tin cậy.
4. Người trả lời có điểm hỏi đáp càng cao thì độ tin cậy của lời giải sẽ càng cao.
5. Các bài có dòng chữ "Câu trả lời này đã được Online Math chọn" là các lời giải tin cậy được (vì đã được duyệt bởi các giáo viên của Online Math.)
6. Các lời giải do chính người đặt câu hỏi chọn cũng là các câu trả lời có thể tin cậy được.
III. Thưởng VIP cho các thành viên tích cực
Online Math hiện có 2 loại giải thưởng cho các bạn có điểm hỏi đáp cao: Giải thưởng chiếc áo in hình logo của Online Math cho 3 - 5 bạn có điểm hỏi đáp cao nhất trong tháng và giải thưởng 1 tháng VIP cho 3 - 5 bạn có điểm hỏi đáp cao nhất trong tuần. Thông tin về các bạn được thưởng tiền được cập nhật thường xuyên tại đây.
TA
1
P
13 tháng 10 2015
128) 4 là một ước của a vì 4 là một ước của 23 ;
8 = 23 là một ước của a;
16 không phải là ước của a;
11 là một ước của a;
20 cũng là ước của a vì 20 = 4 . 5 là ước của 23 . 52 .
127)a) 225 = 32 . 52 chia hết cho 3 và 5;
b) 1800 = 23 . 32 . 52 chia hết cho 2, 3, 5;
c) 1050 = 2 . 3 . 52 . 7 chia hết cho 2, 3, 5, 7;
d) 3060 = 22 . 32 . 5 . 17 chia hết cho 2, 3, 5, 17.
7 tháng 11 2017
Bài 5. Hai đại lượng x và y tỉ lệ thuận với nhau hay không, nếu:
a)
| x | 1 | 2 | 3 | 4 | 5 |
| y | 9 | 18 | 27 | 36 | 45 |
b)
| x | 1 | 2 | 5 | 6 | 9 |
| y | 12 | 24 | 60 | 72 | 90 |
a) Ta có :
vậy x và y là hai đại lượng tỉ lệ thuận.
b) Ta có
nên x và y không tỉ lệ thuận.
Bài 6 trang 55. Thay cho việc đo chiều dài các cuộn dây thép người ta thường cân chúng. Cho biết mỗi mét dây nặng 25 gam.
a) Giả sử mét dây nặng y gam. Hãy biểu diễn y theo x.
b) Cuộn dây dài bao nhiêu mét biết rằng nó nặng 4,5 kg?
Đáp án: 1 m dây nặng 25 g
x m dây nặng y g
a) Vì khối lượng của cuộn dây thép tỉ lệ thuận với chiều dài nên 1/x = 25/y ⇒ y = 25x
b) Đổi 4,5 kg = 4500 g
1/x = 25/4500 ⇒ x = 4500/25 = 180 (m) . Vậy cuộn dây nặng 4,5kg dài 180m.
Bài 7 trang 56 Toán 7. Hạnh và Vân định làm mứt dẻo từ 2,5 kg dâu. Theo công thức, cứ 2 kg dâu thì cần 3 kg đường. Hạnh bảo cần 3,75kg, còn Vân bảo cần 3,25kg. Theo em ai đúng, vì sao?
Đáp án bài 7: Vì khối lượng dâu y(kg) tỉ lệ thuận với khối lượng đường x(kg) nên ta có y = kx.
Theo điều kiện đề bài y = 2 thì x = 3, thay vào công thức ta được 2 = k.3 nên k = 2/3.
Công thức trở thành y = 2/3x
Khi y = 2,5 thì x = 3/2; y = 3/2 . 2,5 = 3,75 Vậy Hạnh nói đúng.Bài 8 trang 56. Học sinh của ba lớp 7 cần phải trồng và chăm sóc 24 cây xanh. Lớp 7A có 32 học sinh, lớp 7B có 28 học sinh, lớp 7C có 36 học sinh. Hỏi mỗi lớp phải trồng và chăm sóc bao nhiêu cây xanh, biết rằng số cây xanh tỉ lệ với số học sinh.
Giải: Gọi số cây trồng của các lớp 7A, 7B, 7C lần lượt là x, y, z. Theo đề bài ta có x + y + z = 24 và số cây xanh và số học sinh tỉ lệ nhau : 
Theo tính chất của dãy tỉ số bằng nhau ta có:
x = 1/4 . 32 = 8;
y = 1/4 . 28 = 7;
z = 1/4 . 36 = 9.
Vậy : số cây xanh của lớp 7A, 7B, 7C là 8, 7, 9 cây xanh.
Bài 9 trang 56 Toán 7 tập 1. Đồng bạch là một loại hợp kim của niken, kẽm, đồng, khối lượng của chúng lần lượt tỉ lệ với 3, 4 và 13. Hỏi cần bao nhiêu kilôgam niken, kẽm, đồng để sản xuât 150 kg đồng bạch.
Giải: Gọi khối lượng (kg) của niken, kẽm, đồng lần lượt là x, y, z. Theo đề bài ta có: x + y + z = 150 và 
Theo tính chất của dãy tỉ số bằng nhau ta có:
Vì vậy x = 7,5.3 = 22,5.
y = 7,5.4 = 30
z = 7,5.13 = 97,5
Vậy khối lượng của niken, kẽm, đồng theo thứ tự là 22,5kg, 30kg, 97,5kg.
Bài 10. Biết các cạnh của một tam giác tỉ lệ với 2; 3; 4 và chu vi của nó là 45 cm. Tính các cạnh của tam giác đó
Giải bài 10:Gọi chiếu dài (cm) của các cạnh của tam giác tỉ lệ với 2, 3, 4 lần lượt là x, y, z.
Theo đề bài, ta có: x/2 = y/3 = z/4 và x + y + z = 45
Theo tính chất của dãy tỉ số bằng nhau ta có:
Nên x = 5.2 = 10
y = 5.3 = 15
z = 5.4 = 20
Vậy các cạnh của tam giác là 10cm, 15cm, 20cm.
Bài 11. Đố em tính được trên một chiếc đồng hồ khi kim giờ quay được một vòng thì kim phút, kim giây quay được bao nhiêu vòng?
Giải: Ta biết rằng 1 giờ = 60 phút = 60.60 = 3600 giây.
Do đó khi kim giờ đi được 1 giờ thì kim phút đi được 1 vòng và kim giây quay được 60 vòng trên mặt đồng hồ.
Vậy trên mặt chiếc đồng hồ khi kim giờ quay được 1 vòng thì kim phút quay được 1.12 = 12 (vòng) và kim giây quay được 60.12 = 720 (vòng).
bạn trả lời câu hỏi giúp mình đi
7 tháng 11 2017
mình biết rồi
ca ngợi hành động của các bạn , chung tay góp sức để bảo vệ môi trường
KS
2
8 tháng 11 2017
Hai tam giác bằng nhau là hai tam giác có các cạnh tương ứng bằng nhau, các góc tương ứng bằng nhau.
Để kí hiệu sự bằng nhau của ΔABC và ΔA’B’C’ ta viết:
∆ABC= ∆A’B’C’.
∆ABC= ∆A’B’C’ nếu
Bài 10. Trong các hình sau các Δ nào bằng nhau(Các cạnh bằng nhau được đánh dấu bởi những kí hiệu giống nhau). Kể tên các đỉnh tương ứng của các Δ bằng nhau đó. Viết kí hiệu về sự bằng nhau của các Δ đó.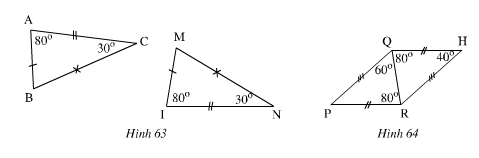
Hình 63:
Ta có:
- ∠A = ∠I = 800;
- ∠C = ∠N = 300
Xét ΔABC ta có: ∠B =1800 – (∠A+∠C)=1800 – (800+300) =700
Xét ΔMIN ta có: ∠M =1800 – (∠I+∠N)=1800 – (800+300) =700
- ⇒∠B = ∠M = 700
Và AB=MI, AC=IN, BC=MN.
nên ∆ABC = ∆IMN
Hình 64:
Ta có:
∠RQH = ∠QRP = 800 (ở vị trí so le trong)
Nên QH // RP
Nên ∠HRQ = ∠PQR = 600(so le trong)
∠P = ∠H = 400
và QH= RP, HR= PQ, QR chung.
nên ∆HQR = ∆PRQ.
Bài 11. Cho ∆ ABC = ∆ HIK
a) Tìm cạnh tương ứng với cạnh BC. Tìm góc tương ứng với ∠H
b) Tìm các cạnh bằng nhau, tìm các góc bằng nhau.
HD: a) Ta có ∆ ABC = ∆ HIK, nên cạnh tương ứng với BC là cạnh IK. Góc tương ứng với ∠H là ∠A.
b) ∆ ABC= ∆ HIK
Suy ra: AB = HI, AC = HK, BC = IK.
∠A = ∠H, ∠B =∠I, ∠C = ∠K.
Bài 12 trang 112. Cho ∆ ABC= ∆ HIK trong đó cạnh AB = 2cm. ∠B=400; BC= 4cm. Em có thể suy ra số đo của những cạnh nào, những góc nào của ΔHIK?
Ta có ∆ ABC= ∆ HIK (gt)
Suy ra: AB = HI= 2cm, BC = IK= 4cm, ∠I = ∠B = 400
Bài 13. Cho ∆ ABC= ∆ DEF. Tính chu vi mỗi tam giá nói trên biết AB = 4cm, BC = 6cm, DF = 5cm (chu vi của một tam giác là tổng độ dài ba cạnh của tam giác đó)
Ta có ∆ABC = ∆ DEF
Suy ra: AB = DE= 4cm, BC = EF = 6cm, DF = AC = 5cm.
Chu vi của ΔABC bằng: AB + BC + AC = 4 + 5 + 6 = 15 (cm)
Chu vi của ΔDEF bằng: DE + EF + DF = 4 + 5 + 6 = 15 (cm )
Bài 14 trang 112. Cho hai tam giác bằng nhau: ΔABC (Không có hai góc nào bằng nhau, không có hai cạnh nào bằng nhau) và một Δ có ba đỉnh H, I ,K. Viết kí hiệu về sự bằng nhau của hai Δ đó biết: AB=KI, ∠B =∠K.
Giải: Ta có: ∠B =∠K nên B, K là hai đỉnh tương ứng.
AB= KI nên A, I là hai đỉnh tương ứng.
Vậy ∆ABC = ∆IKH.
CT
0
TD
4
8 tháng 3 2017
1 ngày có số giây là
24 x 60 x 60 = 86400 (giay)
co so o to di qua la
86400 : 50 = 1728 ô tô
t5k va kbv nha
8 tháng 3 2017
đổi 1 ngày = 24 giờ = 86400 giây
trong một ngày có số lượt ô tô chạy qua cầu là:
86400 : 50 = 1728 lượt
đáp số 1728 lượt
Bn chụp hình lại đi rồi mình giải cho
bài 48
Hình dưới cho biết ˆA=140∘;ˆB=70∘;ˆC=150∘A^=140∘;B^=70∘;C^=150∘
Chứng minh rằng Ax // Cy
Giải
Kẻ tia Bz // Ax và Cy’ là tia đối của tia Cy
Ta có: ˆB2+ˆxAB=180∘B2^+xAB^=180∘ (hai góc trong cùng phía)
Mà ˆxAB=140∘(gt)xAB^=140∘(gt)
Suy ra: ˆB2=180∘−ˆxABB2^=180∘−xAB^
⇒⇒ ˆB2=180∘−140∘=40∘B2^=180∘−140∘=40∘
Mà ˆB1+ˆB2=ˆABCB1^+B2^=ABC^
⇒ˆB1=ˆABC−ˆB2⇒B1^=ABC^−B2^
= 70° - 40° = 30° (1)
ˆyCB+ˆBCy′=180∘yCB^+BCy′^=180∘ (2 góc kề bù)
⇒ˆBCy′=180∘−ˆyCB=180∘−150∘=30∘(2)⇒BCy′^=180∘−yCB^=180∘−150∘=30∘(2)
Từ (1) và (2) suy ra: ˆB1=ˆBCy′B1^=BCy′^
Suy ra: Cy’ // Bz (Vì có cặp góc ở vị trí so le trong bằng nhau)
Hay Cy // Bz mà Bz // Ax suy ra l ; Ax // Cy
bài 49
Hình dưới cho biết ˆA=140∘;ˆB=70∘;ˆC=150∘A^=140∘;B^=70∘;C^=150∘
Chứng minh rằng Ax // Cy
Giải
Kẻ tia Bz // Ax và Cy’ là tia đối của tia Cy
Ta có: ˆB2+ˆxAB=180∘B2^+xAB^=180∘ (hai góc trong cùng phía)
Mà ˆxAB=140∘(gt)xAB^=140∘(gt)
Suy ra: ˆB2=180∘−ˆxABB2^=180∘−xAB^
⇒⇒ ˆB2=180∘−140∘=40∘B2^=180∘−140∘=40∘
Mà ˆB1+ˆB2=ˆABCB1^+B2^=ABC^
⇒ˆB1=ˆABC−ˆB2⇒B1^=ABC^−B2^
= 70° - 40° = 30° (1)
ˆyCB+ˆBCy′=180∘yCB^+BCy′^=180∘ (2 góc kề bù)
⇒ˆBCy′=180∘−ˆyCB=180∘−150∘=30∘(2)⇒BCy′^=180∘−yCB^=180∘−150∘=30∘(2)
Từ (1) và (2) suy ra: ˆB1=ˆBCy′B1^=BCy′^
Suy ra: Cy’ // Bz (Vì có cặp góc ở vị trí so le trong bằng nhau)
Hay Cy // Bz mà Bz // Ax suy ra l ; Ax // Cy