Bài 4: Cho O thuộc đường thẳng AB. Trên cùng một nửa mp bờ AB vẽ các tia OM, ON sao cho AONˆ = BONˆ = 50o. Vẽ tia phân giác của góc MON. Hỏi:
a) Hai tia OM, ON có vuông góc với nhau hay không?
b) CMR: OC⊥AB.
Bài 6: Trên đường thẳng a liên tiếp lấy 5 điểm A, B, C, D, E sao cho AB=BC=CD=DE. Qua C hãy vẽ đường thẳng b⊥a. Hỏi đường thẳng b là đường trung trực của những đường thẳng nào?
Bài 7: Cho hai góc kề bù xOyˆ và yOzˆ. Gọi Om là tia phân giác của góc xOy, vẽ tia Om⊥On. CMR On là tia phân giác của góc xOy.
Bài 8: Trong hình vẽ cho AB // CI. OABˆ = 50o, OCIˆ = 40o. CMR OA⊥OC
Bài 9: Cho góc xOy là góc tù; trong góc này vẽ các tia Om, On sao cho Ox⊥On, Oy⊥Om. CMR: góc xOy và góc MOn có chung tia phân giác
Bài 10: Cho góc bẹt AOB. Trên cùng nửa mp bờ AB vẽ các tia OC và OD sao cho AOCˆ = BODˆ = 135o. Gọi OE là tia đối của tia OD. CMR:
a) OE⊥OC
b) OB là tia phân giác của góc COE.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b) TỪ hình như đề sai thì pk ; aom=bon=50 chứ sao lại aom=mon=50

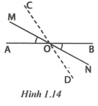
Theo đề bài ta có A O M ^ = M O C ^ , B O N ^ = D O N ^ mà A O M ^ = B O N ^ (hai góc đối đỉnh) nên M O C ^ = D O N ^ .
Ta có M O D ^ + D O N ^ = 180 ° (hai góc kề bù), suy ra M O D ^ + M O C ^ = 180 ° .
Hai góc MOD và MOC là hai góc kề, có tổng bằng 180 ° nên hai tia OC, OD đối nhau.
Chứng tỏ một tia là tia phân giác

\(\Rightarrow\widehat{AOM}=\widehat{BON}\)
\(\Rightarrow\widehat{AOM}+\widehat{MOC}+\widehat{CON}+\widehat{NOB}=180^o\)
Mà: \(\widehat{AOM}=\widehat{BON},\widehat{CON}=\widehat{COM}\)
\(\Rightarrow2\widehat{AOM}+2\widehat{MOC}=180^o\)
\(\Rightarrow\widehat{AOM}+\widehat{MOC}=90^o\Leftrightarrow\widehat{AOC}=90^o\)
\(\Rightarrow CO\perp AB\)

Vì góc AOB là góc bẹt => góc AOB = 180 độ
Vì góc AOM = BON mà OC là tia phân giác của góc MON => MOC = NOC =1/2 MON
=> AOM+MOC=BON+NOC
=> AOC = BOC mà AOC+BOC= AOB
=> AOC = BOC = 180 : 2= 90 độ
=> AOC VÀ BOC là góc vuông và OC cắt AB tại O=> OC vuông góc AB