So sánh hai luỹ thừa bằng cách tính giá trị cụ thể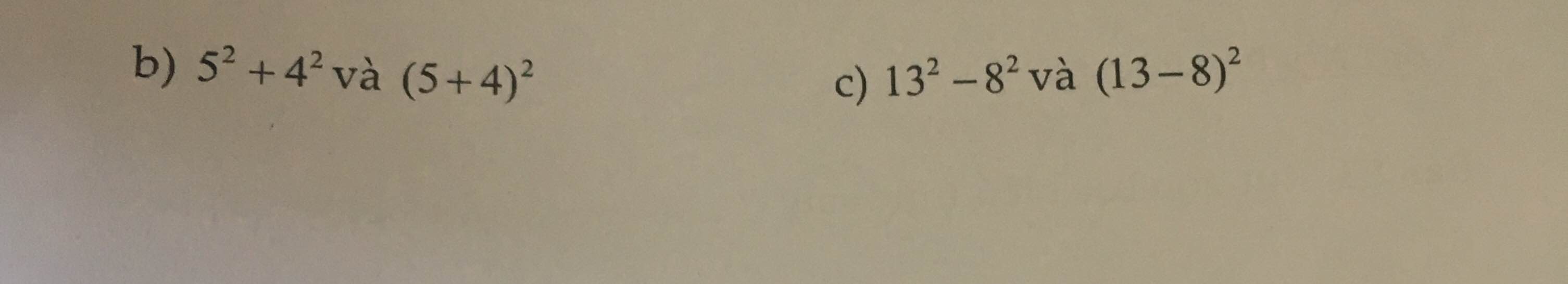
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
5 tháng 11 2018
A = 2019.2021 = (2018+1).2021 = 2018.2021 + 2021.
B = 2018.2022 = 2018.(2021+1) = 2018.2021+2018.
Vì 2018.2021+2021 >2018.2021+2018 nên A > B.
CM
17 tháng 2 2017
A = 2018.2018 - 2018.(2017+1) = 2018.2017 + 2018.
B = 2017.2019 = 2017.(2018+1) = 2017.2018 + 2017.
Vì 2018.2017 + 2018 > 2017.2018 + 2017 nên A > B.
DV
1
26 tháng 9 2015
A = 198 . 202 B = 200 . 200
A = 198 . ( 200+ 2 ) B = (198 + 2 ) . 200
A = 198 . 200 + 198 . 2 B = 198 . 200 + 2 . 200
VI 198 . 2 < 2. 200 NEN A < B
NK
1
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
19 tháng 10 2021
B=2010.2012=(2011-1).(2011+1)=2011.2011-1<2011.2011=A
B
23 tháng 8 2017
a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)
PT
2
8 tháng 9 2015
Ta có :
C = 35 . 53 - 18
= ( 34 + 1 ) . 53 - 18
= 53 . 34 + 53 - 18
= 53 . 34 + 35 = D
Vậy C = D
21 tháng 1 2017
Ta có
C = 35 . 53 - 18
C = ( 34+1 ) . 53 - 18
C = 53 .34 + 53 - 18
C = 53 . 34 + 35
Vậy ta có thể nói C = D
b: \(5^2+4^2=25+16=41\)
\(\left(5+4\right)^2=9^2=81\)
mà 41<81
nên \(5^2+4^2< \left(5+4\right)^2\)
c: \(13^2-8^2=169-64=105\)
\(\left(13-8\right)^2=5^2=25\)
mà 105>25
nên \(13^2-8^2>\left(13-8\right)^2\)
\(b,\)\(5^2+4^2\)\(=25+16\) \(=41\)
\(\left(5+4\right)^2=9^2=81\)
\(mà\) \(41< 81\)
\(nên\) \(5^2+4^2< \left(5+4\right)^2\)