Bài 1 Cho hình vuông ABCD nối tiếp đường tròn tâm O, cạnh hình vuông bằng \(\sqrt{2}\)cm. Tính khoảng cách từ tâm O đến dây AB. So sánh khoảng cách từ tâm O đến các dây BC,CD,DA
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
26 tháng 7 2018
Gọi H và K lần lượt là hình chiếu của O trên AB và CD
Tính được OH = MK = 3cm
OD = OB = 3 10 cm
Từ đó tính được OK = 41 cm
CM
1 tháng 7 2017
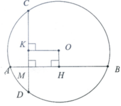
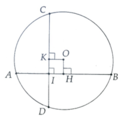
Gọi OH,OK là khoảng cách từ O đến mỗi dây
Ta có: OH = OK = 1cm
Tính được R = 10 cm
CM
13 tháng 5 2019
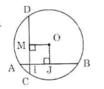
a) Kẻ OJ vuông góc với AB tại J.
Theo quan hệ vuông góc giữa đường kính và dây suy ra: J là trung điểm của AB.
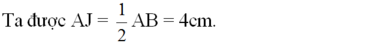
Áp dụng định lí Pitago trong tam giác vuông OAJ có:
OJ2 = OA2 – AJ2 = 52 – 42 = 9 (OA = R = 5cm)
=> OJ = 3cm (1)
Vậy khoảng cách từ tâm O đến dây AB là OJ = 3cm.
b) Kẻ OM vuông góc với CD tại M.
Tứ giác OJIM có: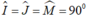 
nên là hình chữ nhật
Ta có IJ = AJ – AI = 4 – 1 = 3cm
=> OM = IJ = 3cm (Tính chất hình chữ nhật) (2)
Từ (1), (2) suy ra CD = AB (hai dây cách đều tâm thì bằng nhau). (đpcm)
Dựng các đường kính MH,KN như hình :
Tứ giác ABNK có 4 góc vuông nên :
\(\Rightarrow\)Tứ giác ABNK là hình chữ nhật
Ta có :
\(\hept{\begin{cases}ON=OK\\AM=MB\end{cases}}\)
\(\Rightarrow\)MO là đường trung bình
\(\Rightarrow MO=\frac{BN+AK}{2}=\frac{\frac{1}{2}AB+\frac{1}{2}AD}{2}=\frac{\frac{1}{2}BC}{2}\)
\(=\frac{BC}{2}=\frac{\sqrt{2}}{2}\)
Ta có :
\(OM\perp AB,OH\perp CD,OK\perp AD,ON\perp BC\)
\(\Rightarrow\)MNHK \(\in\left(O\right)\)nội tiếp hình vuông
\(\Rightarrow OM=OH=OK=ON=\frac{\sqrt{2}}{2}\)