cc giúp mk làm bài này với ,cảm ơn trước nhá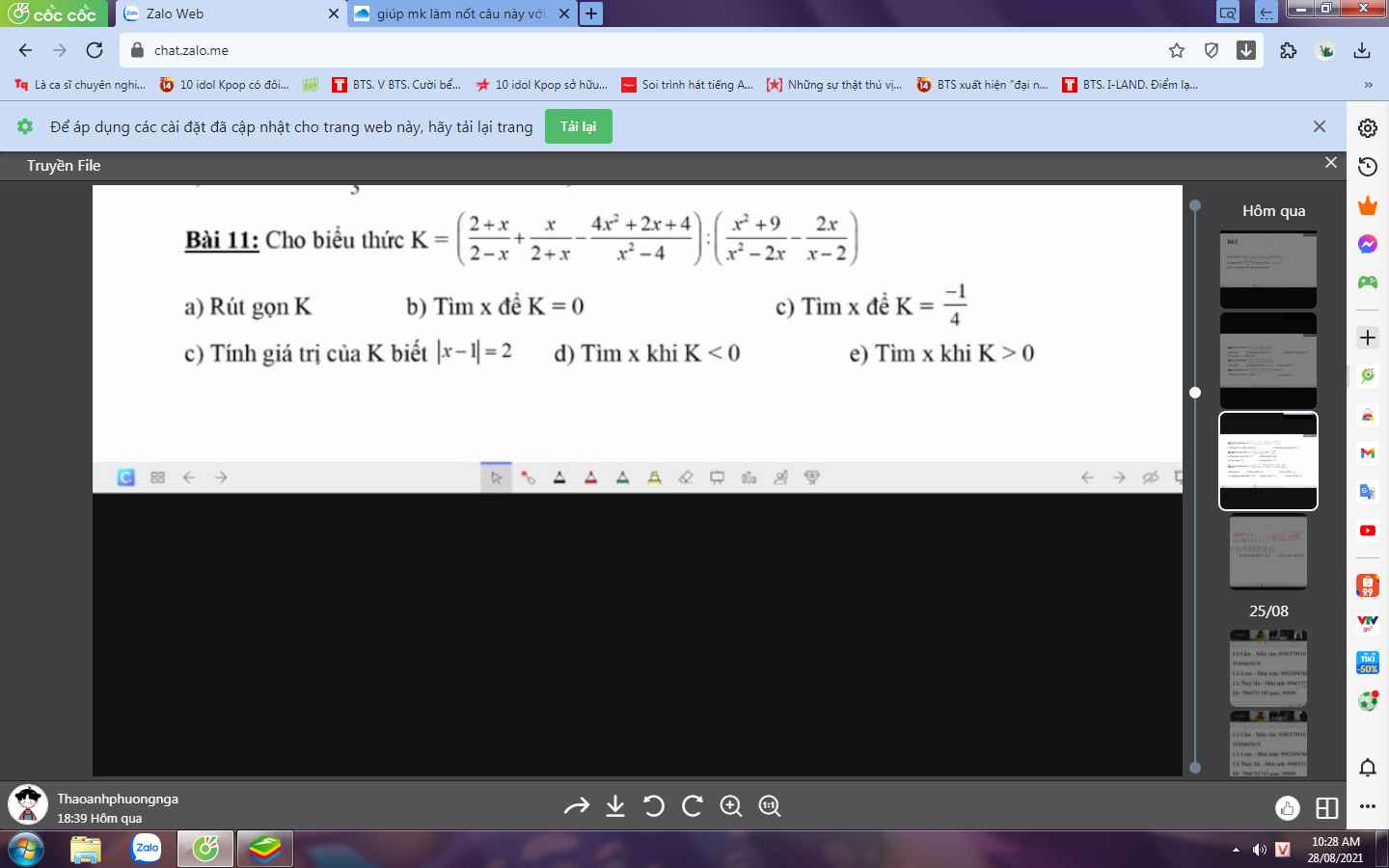
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
28 tháng 8 2021
a. ĐKXĐ: \(x\ge4\)
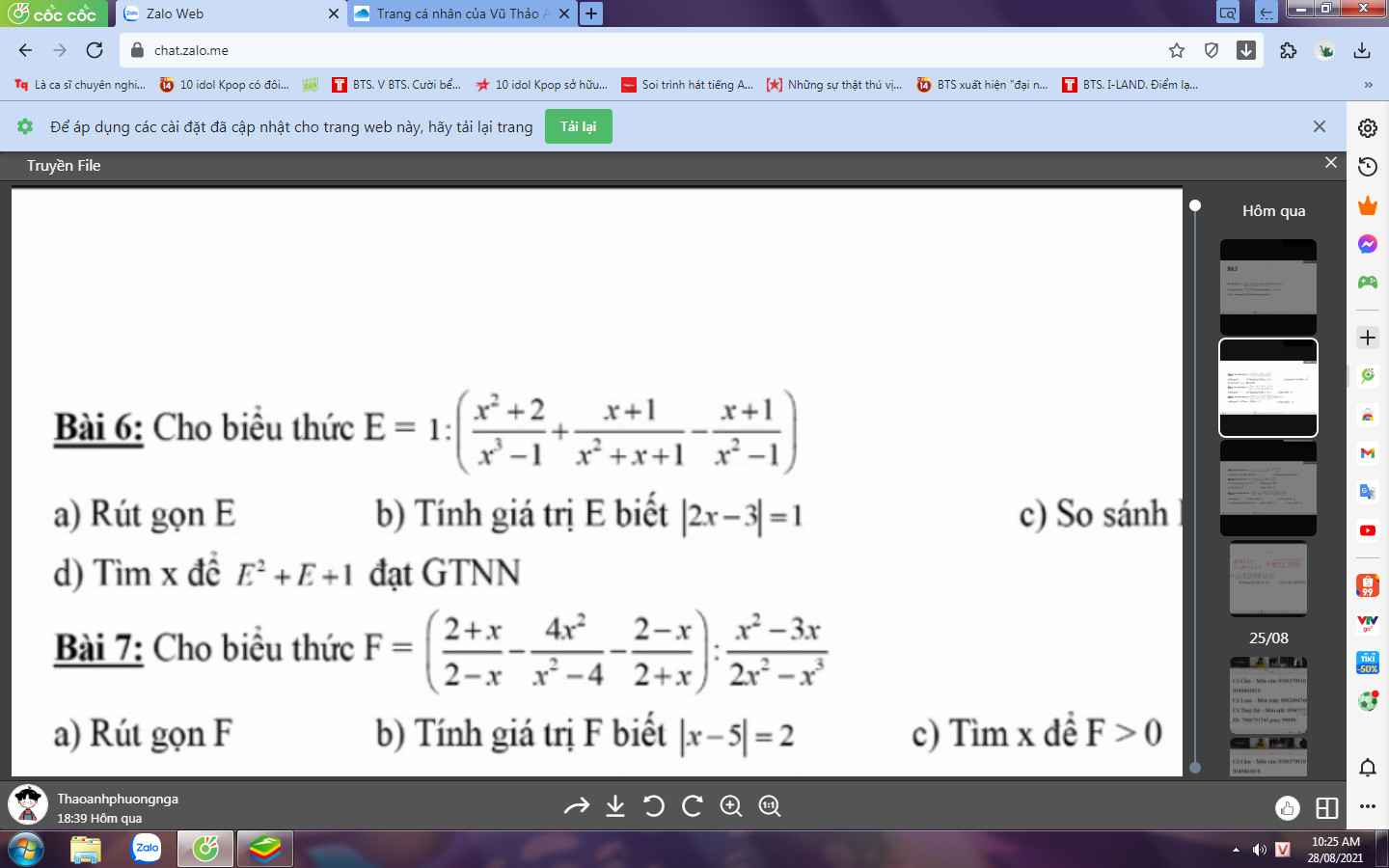
\(F=\left(\dfrac{2+x}{2-x}-\dfrac{4x^2}{x^2-4}-\dfrac{2-x}{2+x}\right):\dfrac{x^2-3x}{2x^2-x^3}\)
\(=\left(\dfrac{\left(2+x\right)\left(2+x\right)}{\left(2-x\right)\left(2+x\right)}+\dfrac{4x^2}{\left(2-x\right)\left(2+x\right)}-\dfrac{\left(2-x\right)\left(2-x\right)}{\left(2-x\right)\left(2+x\right)}\right):\dfrac{x\left(x-3\right)}{x^2\left(2-x\right)}\)
\(=\dfrac{4+4x+x^2+4x^2-4+4x-x^2}{\left(2-x\right)\left(2+x\right)}.\dfrac{x^2\left(2-x\right)}{x\left(x-3\right)}\)
\(=\dfrac{4x^2+8x}{\left(2-x\right)\left(2+x\right)}.\dfrac{x^2\left(2-x\right)}{x\left(x-3\right)}=\dfrac{4x\left(x+2\right)x^2\left(2-x\right)}{\left(x+2\right)\left(2-x\right)x\left(x-3\right)}=\dfrac{4x^2}{x-3}\)
b. Ta có \(\left|x-5\right|=2\) \(\Leftrightarrow\left[{}\begin{matrix}x-5=2\\5-x=2\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=7\\x=3\end{matrix}\right.\)
* Với \(x=7\), ta có biểu thức \(F=\dfrac{4.7^2}{7-3}=\dfrac{196}{4}=49\)
* Với \(x=3\), ta có biểu thức \(F=\dfrac{4.3^2}{3-3}=\dfrac{36}{0}\), lúc này biểu thức không xác định
c. \(F>0\Leftrightarrow\dfrac{4x^2}{x-3}>0\), vì \(4x^2\ge0\forall x\) nên để \(\dfrac{4x^2}{x-3}>0\) thì \(\left\{{}\begin{matrix}4x^2>0\\x-3>0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x>0\\x>3\end{matrix}\right.\) \(\Leftrightarrow x>3\)
AH
Akai Haruma
Giáo viên
28 tháng 8 2021
\(4x^2>0\) thì không tương đương với \(x>0\) mà tương đương với \(x\ne0\)
AH
Akai Haruma
Giáo viên
28 tháng 8 2021
Lời giải:
a.
\(G=\frac{x^2-4}{x+1}+\frac{2}{x+1}:\frac{(2x-3)(x+1)-(2x+1)(x-1)}{(x-1)(x+1)}\)
\(=\frac{x^2-4}{x+1}+\frac{2}{x+1}:\frac{-2}{(x-1)(x+1)}=\frac{x^2-4}{x+1}+\frac{2}{x+1}.\frac{(x+1)(x-1)}{-2}\)
\(=\frac{x^2-4}{x+1}-(x-1)=\frac{x^2-4-(x^2-1)}{x+1}=\frac{-3}{x+1}\)
b.
Để $A\in\mathbb{Z}^+$ thì $x+1$ là ước âm của $-3$
$\Rightarrow x+1\in\left\{-1;-3\right\}$
$\Leftrightarrow x\in\left\{-2;-4\right\}$ (tm)
c.
$G< -1\Leftrightarrow \frac{-3}{x+1}+1< 0$
$\Leftrightarrow \frac{x-2}{x+1}< 0$
$\Leftrightarrow x-2<0< x+1$ hoặc $x-2>0>x+1$
$\Leftrightarrow -1< x< 2$ (chọn) hoặc $-1> x>2$ (loại)
Vậy $-1< x< 2$ và $x\neq 1$
28 tháng 8 2021
Bài 8:
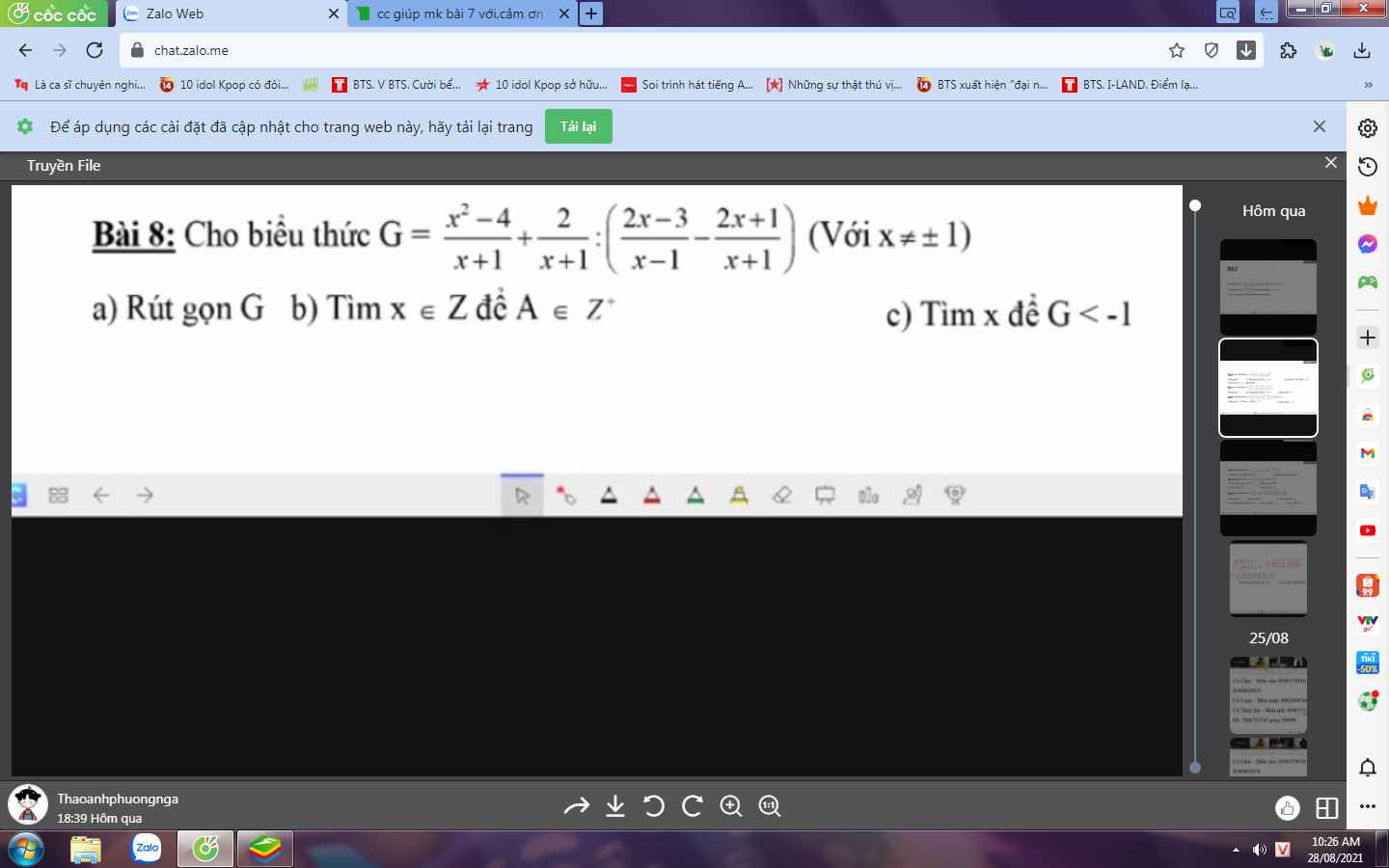
a: Ta có: \(G=\dfrac{x^2-4}{x+1}+\dfrac{2}{x+1}:\left(\dfrac{2x-3}{x-1}-\dfrac{2x+1}{x+1}\right)\)
\(=\dfrac{x^2-4}{x+1}+\dfrac{2}{x+1}:\dfrac{2x^2+2x-3x-3-2x^2+2x-x+1}{\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{\left(x-2\right)\left(x+2\right)}{x+1}+\dfrac{2}{x+1}\cdot\dfrac{\left(x-1\right)\left(x+1\right)}{-2}\)
\(=\dfrac{\left(x-2\right)\left(x+2\right)}{x+1}+\dfrac{-x+1}{1}\)
\(=\dfrac{x^2-4-\left(x-1\right)\left(x+1\right)}{x+1}\)
\(=\dfrac{x^2-4-x^2+1}{x+1}\)
\(=-\dfrac{3}{x+1}\)
giúp mk làm nốt mấy câu này với,cảm ơn trước nhá
27 tháng 8 2021
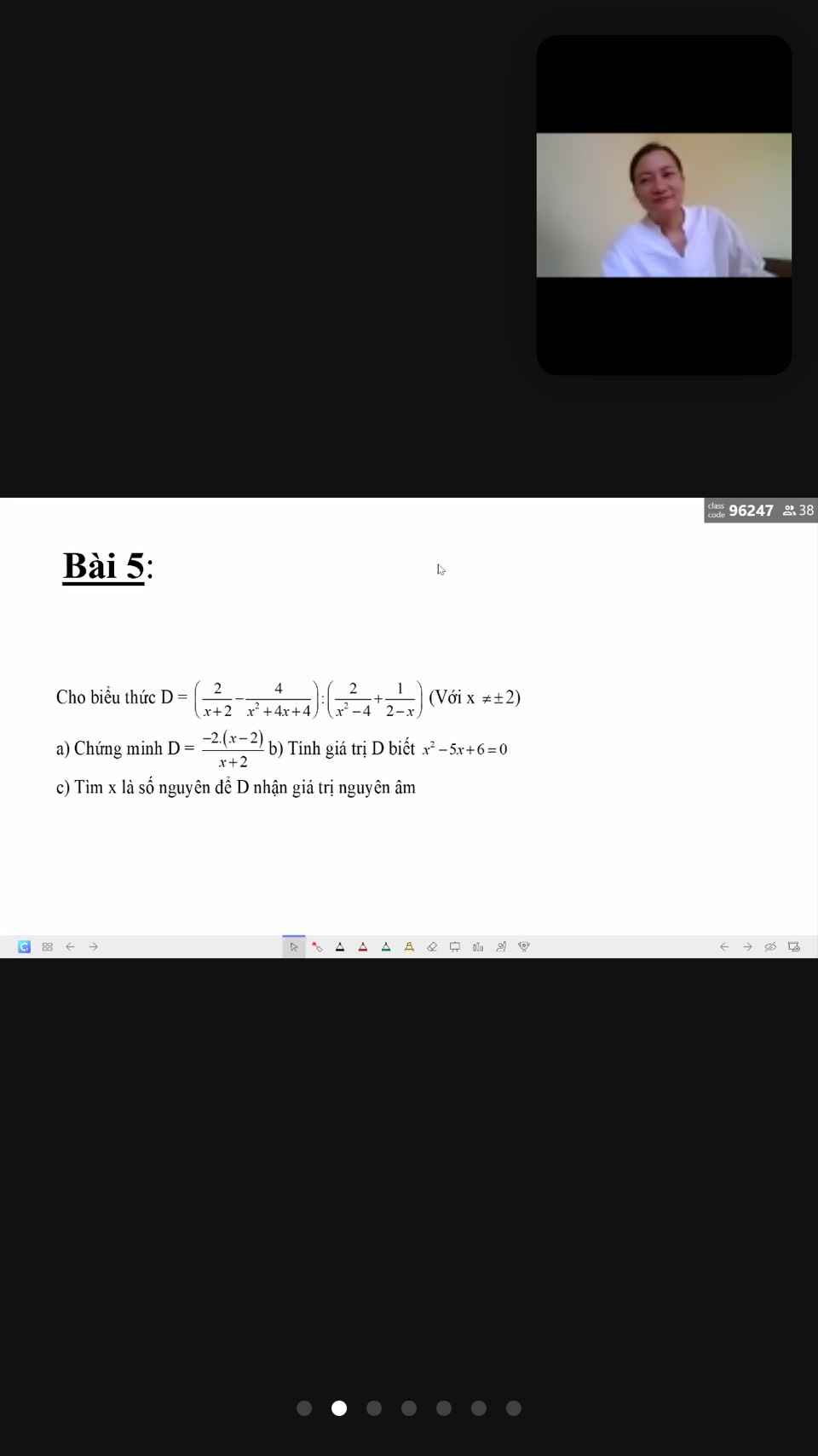
a) \(D=\left(\dfrac{2}{x+2}-\dfrac{4}{x^2+4x+4}\right):\left(\dfrac{2}{x^2-4}+\dfrac{1}{2-x}\right)\)\(=\left(\dfrac{2}{x+2}-\dfrac{4}{\left(x+2\right)^2}\right):\left(\dfrac{2}{\left(x-2\right)\left(x+2\right)}-\dfrac{1}{x-2}\right)\)
\(=\left(\dfrac{2\left(x+2\right)}{\left(x+2\right)^2}-\dfrac{4}{\left(x+2\right)^2}\right):\left(\dfrac{2}{\left(x-2\right)\left(x+2\right)}-\dfrac{x+2}{\left(x-2\right)\left(x+2\right)}\right)\)
\(=\dfrac{2\left(x+2\right)-4}{\left(x+2\right)^2}:\dfrac{2-x-2}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{2x+4-4}{\left(x+2\right)^2}:\dfrac{-x}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{2x}{\left(x+2\right)^2}.\dfrac{\left(x-2\right)\left(x+2\right)}{-x}\)
\(=\dfrac{-2.\left(x-2\right)}{x+2}\)
\(x^2-5x+6=0\\ \Rightarrow\left(x^2-2x\right)-\left(3x-6\right)=0\\ \Rightarrow\left(x-2\right)\left(x-3\right)=0\\ \Rightarrow\left[{}\begin{matrix}x-2=0\\x-3=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=2\\x=3\end{matrix}\right.\)
\(P=\dfrac{-2.\left(x-2\right)}{x+2}\)
Thay \(x=2\), ta có:
\(P=\dfrac{-2.\left(2-2\right)}{2+2}\)
\(=0\)
Thay \(x=3\), ta có:
\(P=\dfrac{-2.\left(3-2\right)}{3+2}\)
\(=-\dfrac{2}{5}\)
28 tháng 8 2021
a) Ta có:
\(H=\left(\dfrac{x}{x^2-4}+\dfrac{1}{x+2}+\dfrac{2}{2-x}\right):\left(x-2+\dfrac{10-x^2}{x+2}\right)\\ =\left(\dfrac{x}{x^2-4}+\dfrac{x-2}{x^2-4}-\dfrac{2\left(x+2\right)}{x^2-4}\right):\left(\dfrac{x^2-4+10-x^2}{x+2}\right)\\ =\dfrac{x+x-2-2x-4}{\left(x-2\right)\left(x+2\right)}\cdot\dfrac{x+2}{6}\\ =\dfrac{-6}{x-2}\cdot\dfrac{1}{6}=\dfrac{1}{2-x}\)
b) Để H < 0 thì \(\dfrac{1}{2-x}\) < 0 hay 2 - x < 0 ( do 1 > 0) suy ra x > 2
Vậy với x > 2 thì H < 0.
c) Ta có:
\(\left|x\right|=3\\ \Leftrightarrow\left[{}\begin{matrix}x=3\\x=-3\end{matrix}\right.\)
+) Với x = 3 thì:
H = \(\dfrac{1}{2-3}=-1\)
+) Với x = -3 thì:
\(H=\dfrac{1}{2-\left(-3\right)}=\dfrac{1}{5}\)
Vậy với |x| = 3 thì H = -1 hoặc H = 1/5
28 tháng 8 2021
a: Ta có: \(H=\left(\dfrac{x}{x^2-4}+\dfrac{1}{x+2}+\dfrac{2}{2-x}\right):\left(x-2+\dfrac{10-x^2}{x+2}\right)\)
\(=\dfrac{x+x-2-2x-4}{\left(x-2\right)\left(x+2\right)}:\dfrac{x^2-4+10-x^2}{x+2}\)
\(=\dfrac{-6}{\left(x-2\right)\left(x+2\right)}\cdot\dfrac{x+2}{6}\)
\(=\dfrac{-1}{x-2}\)
b: Để H<0 thì x-2<0
hay x<2
Kết hợp ĐKXĐ, ta được: \(\left\{{}\begin{matrix}x< 2\\x\ne-2\end{matrix}\right.\)
28 tháng 8 2021
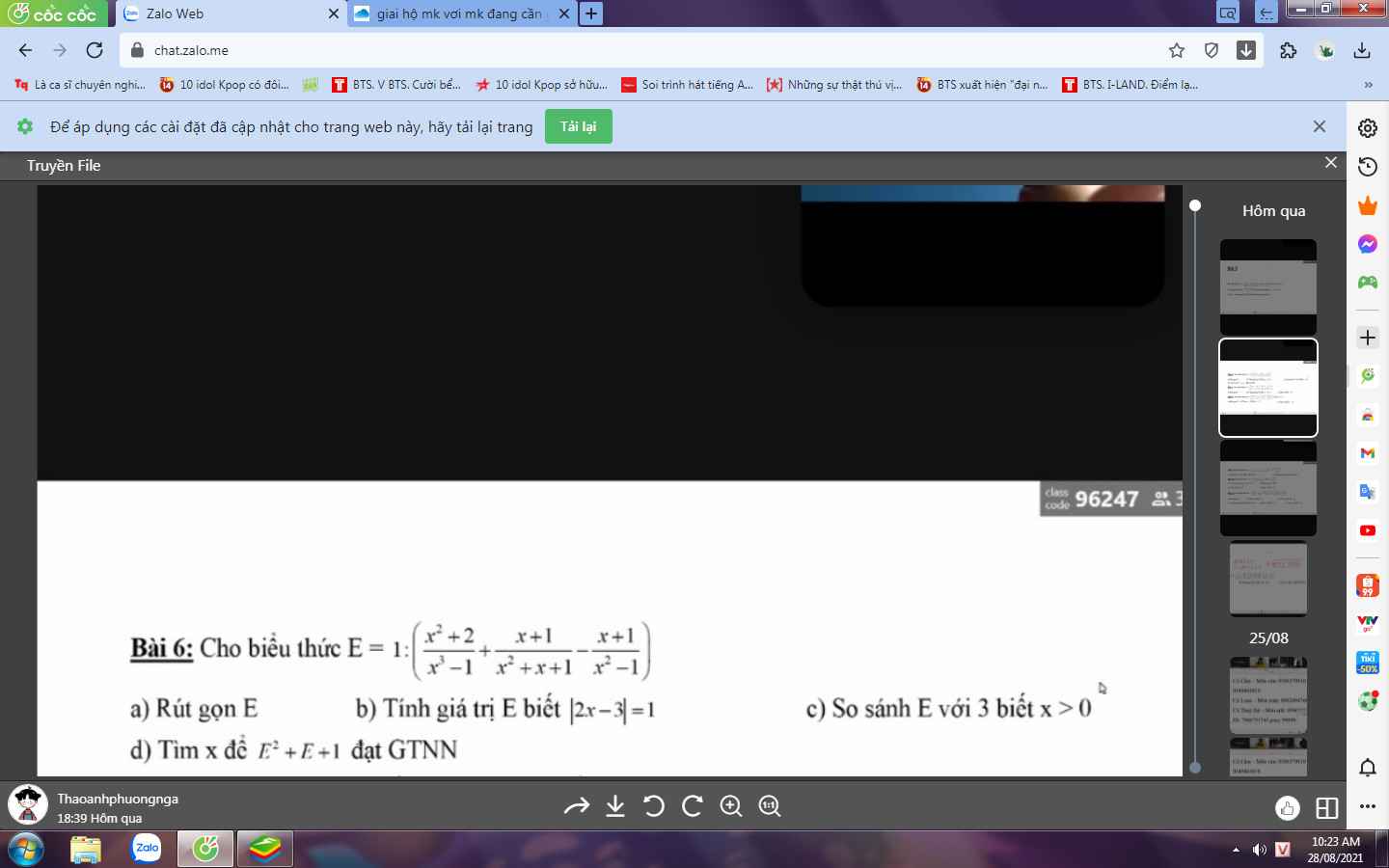
Bài 6:
a: Ta có: \(E=1:\left(\dfrac{x^2+2}{x^3-1}-\dfrac{x+1}{x^2+x+1}-\dfrac{x+1}{x^2-1}\right)\)
\(=1:\left(\dfrac{x^2+2}{\left(x-1\right)\left(x^2+x+1\right)}-\dfrac{x+1}{x^2+x+1}-\dfrac{1}{x-1}\right)\)
\(=1:\dfrac{x^2+2-x^2+1-x^2-x-1}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{\left(x-1\right)\left(x^2+x+1\right)}{-x^2-x+2}\)
\(=\dfrac{-\left(x-1\right)\left(x^2+x+1\right)}{\left(x+2\right)\left(x-1\right)}\)
\(=\dfrac{-x^2-x-1}{x+2}\)
TL
17 tháng 2 2019
Dân tộc Việt Nam vốn có truyền thống nhân nghĩa thuỷ chung son sắt. Lòng biết ơn đôi với người khác - người có công ơn với mình là một biểu hiện của truyền thống nhân nghĩa đó. Đểghi nhớ và nhắc nhở con cháu đời sau, cha ông xưa đã đúc kết và lưu truyền trong những câu tục ngữ vô cùng ý nghĩa:
Ăn quả nhớ kẻ trồng cây
Uống nước nhớnguồn
Tuylà hau câu tục ngữ khác nhau, cách diễn đạt cũng khác nhau nhưng cả hai đều chứa đựng bài học luân lí về cách sống, về tình nghĩa cao đẹp của người Việt Nam với nhau. Khi ăn trái ngon ngọt, ta phải nhớ ơn người đã dàv công vun trồng, chăm sóc từ khi cây còn con đến lúc ra quả ngọt trái chín. Được uống ngụm nước trong lành, mát lạnh, nhất định ta không được quên cội nguồn - nơi dòng nước chảy tới. Vẫn là đặc điểm quen thuộc của tục ngữ, vẫn là những hình ảnh tượng trưng độc đáo và hàm súc, cha ông ta gửi gắm vào đó lời răn dạy về lòng biết ơn: người được hưởng thành quả lao động thì phải biết ơn người tạo ra nó. Đểcó được cuộc sống như ngày hôm nay, ta không được quên ơn những người đã mang đến cho ta sự ấm no hạnh phúc.
Truyền thống “Uống nước nhớ nguồn”, “Ăn quả nhớ kẻ trồng cây” vốn đã đi vào đời sống, là nét đẹp trong phẩm chất của người Việt. Gần gũi làthờ cúng ông bà tổ tiên mỗi khi tết, giỗ trong mỗi gia đình để tỏ lòng biết ơn công lao sinh thành dưỡng dục của con cháu, rầm rộ hơn là những lễ hội được tổ chức hàng năm tưởng nhớ các vị anh hùng dân tộc. Bác Hồ đã dạy: “Các vua Hùng đã có công dựng nước, Bác cháu ta phải cùng nhau giữ lấy nước”. Vì thế mà:
Dù ai đi ngược về xuôi
Nhớ ngày giỗ Tổ mùng mười tháng ba.
Cứ đến dịp lễ hội đền Hùng (Phú Thọ), nhân dân cả nước lại nô nức kéo nhau về nơi quê cha đất tổ để tưởng nhớ công lao dựng nước của vua Hùng, ởmỗi làng, mỗi thôn xóm vẫn diễn ra hoạt động hội làng đều đặn nhằm ghi tạc công lao của các vị thành hoàng làng, tổ nghề, tổ sư.
Để có được cuộc sống ấm no như ngày hôm nay, cha ông ta đã phải đổ mồ hôi, xương máu và cả tính mạng của mình để giữ vững bình yên cho đất nước. Từ thời “mang gươm đi mở cõi” lịch sử của Việt Nam đã là lịch sử dựng nước gắn liền với giữ nước. Hai Bà Trưng, Trần Hưng Đạo, Lê Lợi, Quang Trung... đều trở thành những tên phố, tên đường, tên trường học... luôn nhắc nhở chúng ta về sự đóng góp to lớn của họ cho đất nước. Khắp các địa phương trên cả nước, đền thờ các vị anh hùng dân tộc đều là những di tích lịch sử, trở thành nơi thăm viếng của cả khách trong nước và ngoài nước. Toàn thểnhân dân Việt Nam một lòng biết ơn Đảng, cách mạng và Bác Hồ. Hàng năm, chúng ta có ngày 27/7 - ngày Thương binh liệt sĩ đểtỏ lòng biết ơntới những anh hùng có công với cách mạng, lòng biết ơn được thể hiện bằng hành động rất cụ thể như phong trào “đền ơn đáp nghĩa”,, “nhà tình nghĩa”... Xã hội cũng có nhiều chính sách ưuđãi, hỗ trợ, giúp đỡ gia đình thương binh liệt sĩ, bà mẹ Việt Nam anh hùng.
Gần gũi với học sinh nhất là ngày 20-11 - ngày Hiến chương các nhà giáo Việt Nam. Tục ngữ có câu “nhất tự vi sư, bán tự vi sư”, “không thầy đố mày làm nên” là để nói về công lao to lớn của thầy cô giáo đối với các thế hệ học trò. Vì thế cứ mỗi dịp 20-11 hàng năm, học sinh cả nước lại hân hoan bày tỏ lòng biết ơn, yêu kính của mình đối với thầy cô. Trong tình cảm ấy, lòng biết ơn ấy không chỉ thể hiện vào dịp lễ tết, ngày nhà giáo Việt Nam mà phải thực hiện bằng sự tôn trọng, vâng lời thầy cô mỗi giờ lên lớp, bằng kết quả học tập tốt và trong suốt cả cuộc đời.
Những phong tục, lễ hội đáng quý ấy đã trở thành hoạt động không thểthiếu hàng năm của người Việt Nam. Bởi, nhớ ơn Người mang lại cho mình cuộc sống ấm no hạnh phúc trở thành lễ tự nhiên, trở thành nếp sống, nếp nghĩ và phẩm chất tốt đẹp của nhân dân ta. Đó cũng là một trong những đạo lí làm người của dân tộc Việt Nam. Đối với người học sinh thể hiện lòng biết ơn ông bà cha mẹ, thầy cô bằng hành động cụ thể chính là đang thực hiện đạo lí làm người ấy.
17 tháng 2 2019
đừng chép mạng nha,mí bạn chép mạng thì mk hỏi làm j nx
2T
1
XM
23 tháng 3 2022
1. What size shoes do you take?
2. What newspaper do you read?
3. What color are your eyes?
4. What time did you arrive this morning?
5. What kind of film do you like?
6. How tall is your teacher?
7. How far is it from your house to the office?
8. How much did you pay for your new shirt?
9. How often do you take an English test in class?
10. How long have you been studying English?
8 tháng 11 2019
\(B=|2014-2x|+|2016-2x|\)
\(=|2014-2x|+|2x-2016|\ge|2014-2x+2x-2016|\)
Hay \(B\ge2\)
Dấu"="xảy ra \(\Leftrightarrow\left(2014-2x\right)\left(2x-2016\right)\ge0\)
\(\Leftrightarrow\hept{\begin{cases}2014-2x\ge0\\2x-2016\ge0\end{cases}}\)hoặc \(\hept{\begin{cases}2014-2x< 0\\2x-2016< 0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}2x\le2014\\2x\ge2016\end{cases}\left(loai\right)}\)hoặc\(\hept{\begin{cases}2x>2014\\2x< 2016\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x>1007\\x< 1008\end{cases}}\)
\(\Leftrightarrow1007< x< 1008\)
Vậy \(B_{min}=2\)\(\Leftrightarrow1007< x< 1008\)
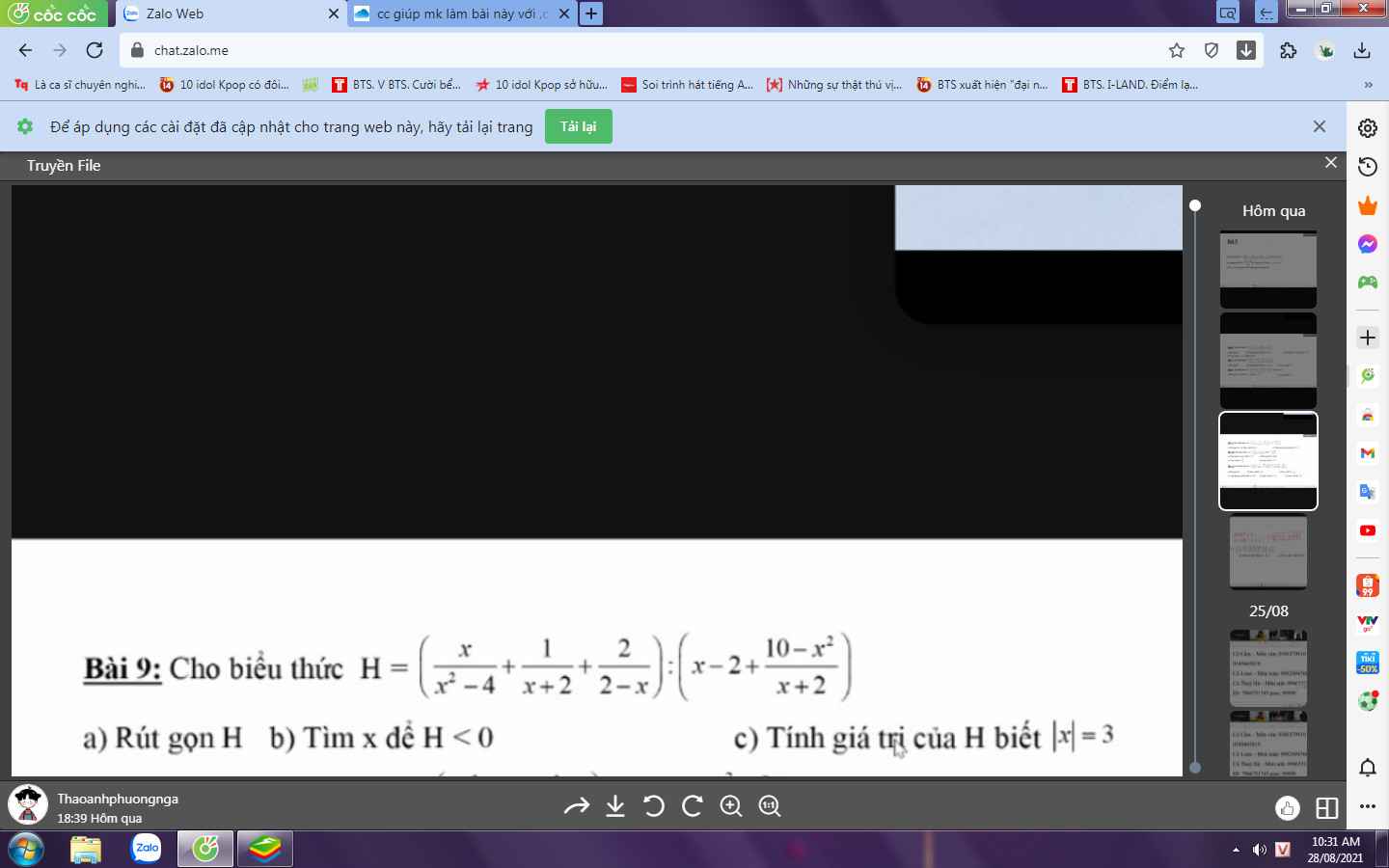
a: Ta có: \(K=\left(\dfrac{2+x}{2-x}+\dfrac{x}{2+x}-\dfrac{4x^2+2x+4}{x^2-4}\right):\left(\dfrac{x^2+9}{x^2-2x}-\dfrac{2x}{x-2}\right)\)
\(=\dfrac{-x^2-4x-4+x^2-2x-4x^2-2x-4}{\left(x-2\right)\left(x+2\right)}:\dfrac{x^2+9-2x^2}{x\left(x-2\right)}\)
\(=\dfrac{-4x^2-8x-8}{\left(x-2\right)\left(x+2\right)}\cdot\dfrac{x\left(x-2\right)}{-x^2+9}\)
\(=\dfrac{-4\left(x^2+2x+1\right)}{x+2}\cdot\dfrac{x}{-\left(x-3\right)\left(x+3\right)}\)
\(=\dfrac{-4x\left(x+1\right)^2}{-\left(x-3\right)\left(x+3\right)\left(x+2\right)}\)