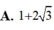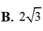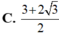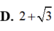xếp 3 viên bi đỏ khác bán kính và 3 viên bi xanh cùng bán kính vào 7 ô trống . hỏi có bao nhieu cách xếp khác nhau
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
25 tháng 1 2018
Bước 1: Xếp 3 bi đỏ khác nhau vào hộp có 7 ô trống có cách.
Bước 2: Xếp 3 bi xanh vào 4 ô trống còn lại,có 
cách.
Theo quy tắc nhân ta có 
cách.
Chọn C.
CM
17 tháng 10 2019
Vì 3 bi đỏ đứng cạnh nhau gọi nhóm 3 bi đỏ là X, và 3 bi xanh đứng cạnh nhau nên gọi nhóm 3 bi xanh là Y.
Vì xếp vào hộc có 7 ô, có 3 viên bi đỏ chiếm 3 vị trí và 3 viên bi xanh chiếm 3 vị trí, còn lại 1 vị trí trống.
Bước 1: Ta xem chỉ có 3 vị trí để xếp X và Y, có A 3 2 cách.
Bước 2: Ứng với mỗi cách xếp ở bước 1, có 3! cách xếp 3 viên bi đỏ khác nhau, còn 3 viên bi xanh chỉ 1 cách xếp vì chúng giống nhau.
Theo quy tắc nhân có A 3 2 . 3 ! = 36 cách xếp thỏa yêu cầu.
Chọn D.
CM
22 tháng 2 2017
Số cách chọn 9 viên tùy ý là C 18 9 .
Những trường hợp không có đủ ba viên bi khác màu là:
* Không có bi đỏ: Khả năng này không xảy ra vì tổng các viên bi xanh và vàng là 8.
* Không có bi xanh: Có C 13 9 cách.
* Không có bi vàng: Có C 15 9 cách.
Mặt khác trong các cách chọn không có bi xanh, không có bi vàng thì C 10 9 cách chọn 9 viên bi đỏ được tính hai lần.
Vậy số cách chọn 9 viên bi có đủ cả ba màu là:
C 10 9 + C 18 9 - C 13 9 - C 15 9 = 42910
Đáp án D
CM
24 tháng 4 2018
Đáp án là C
Số các hoán vị về màu bi khi xếp thành dãy là 3!
Số cách xếp 3 viên bi đen khác nhau thành dãy là 3!
Số cách xếp 4 viên bi đỏ khác nhau thành dãy là 4!
Số cách xếp 5 viên bi xanh khác nhau thành dãy là 5!
Số cách xếp các viên bi trên thành một dãy sao cho các viên bi cùng màu ở cạnh nhau là 3!. 3!. 4!. 5! = 103680 cách.
