Cho (O) và 2 dây EF và CD bằng nhau và vuông góc với nhau tại I. Biết IC = 2cm,ID = 14cm. Tính khoảng cách từ O đến mỗi dây
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

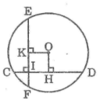
Kẻ OH ⊥ CD, OK ⊥ EF
Vì tứ giác OKIH có ba góc vuông nên nó là hình chữ nhật.
Ta có: CD = EF (gt)
Suy ra: OH = OK (hai dây bằng nhau cách đều tâm)
Suy ra tứ giác OKIH là hình vuông.
Ta có:
CD = CI + ID = 2 + 14 = 16(cm)
HC = HD = CD/2 = 8 (cm) (đường kính dây cung)
IH = HC - CI = 8 - 2 = 6 (cm)
Suy ra: OH = OK = 6 (cm) (OKIH là hình vuông)

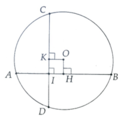
Gọi OH,OK là khoảng cách từ O đến mỗi dây
Ta có: OH = OK = 1cm
Tính được R = 10 cm