Cho điểm A nằm ngoài đường thẳng d và cách d 1 khoảng =2cm .Lấy điểm B bất kì thuộc đường thẳng d. Gọi C là điểm thuộc tia đối của tia BA sao cho BC=BA. Khi điểm B di chuyển lên đường d thì điểm C di chuyển trên đường nào?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
F
9 tháng 9 2020
Tự vẽ hình:)
Kẻ \(AH,CK\perp d\)
Xét \(\Delta vgAHB\)và \(\Delta vgCKB\)có
\(BC=BA\left(gt\right)\)
\(\widehat{ABH}=\widehat{CBK}\left(đ^2\right)\)
\(\Rightarrow\Delta ABH=\Delta CKB\left(ch-gn\right)\)
\(\Rightarrow CK=AH=2cm\)
Điểm C cách đg thg d 1 khoảng 2cm=>C di chuyển trên đg thg m // d và cách d 1 khoảng =2cm
5 tháng 9 2017
Kẻ AH và CK vuông góc với d.
Ta có AB = CB (gt)
=
( đối đỉnh)
nên ∆AHB = ∆CKB (cạnh huyền - góc nhọn)
Suy ra CK = AH = 2cm
Điểm C cách đường thẳng d cố định một khoảng cách không đổi 2cm nên C di chuyển trên đường thẳng m song song với d và cách d một khoảng bằng 2cm.
CM
25 tháng 3 2017
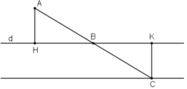
Gọi H, K là hình chiếu của A và C trên đường thẳng d.
⇒ Khoảng cách từ A đến d bằng AH
⇒ AH = 2cm.
Xét ΔAHB vuông tại H và ΔCKB vuông tại K có:
AB = BC
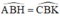
⇒ ΔAHB = ΔCKB (cạnh huyền – góc nhọn)
⇒ CK = AH = 2cm.
Vậy điểm C nằm trên đường thẳng song song với d, không đi qua A và cách d 2cm.
21 tháng 4 2017
Bài giải:
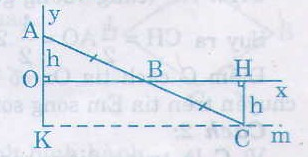
Kẻ AH và CK vuông góc với d.
Ta có AB = CB (gt)
ˆABHABH^ = ˆCBKCBK^ ( đối đỉnh)
nên ∆AHB = ∆CKB (cạnh huyền - góc nhọn)
Suy ra CK = AH = 2cm
Điểm C cách đường thẳng d cố định một khoảng cách không đổi 2cm nên C di chuyển trên đường thẳng m song song với d và cách d một khoảng bằng 2cm.
9 tháng 9 2017
Qua C kẻ a' // d. Xét tam giác vuông DAB và ECB có AB=BC, góc EBC = góc ABD nên chúng bằng nhau. Suy ra AD=EC=2cm. Vậy B chạy trên d thì C chạy trên đường thẳng song song với d cách d một khoảng bằng 2 cm
K
23 tháng 8 2019
Bài làm:
Kẻ AH và CE vuông góc với đường thẳng d.
Xét ΔAHB và ΔCEB, có:
- ABHˆ = EBCˆ (đối đỉnh)
- AB = CB (gt)
- AHBˆ = BECˆ (= 900)
Do đó ΔAHB = ΔCEB (g.c.g)
⇒ CE = AH = 2cm(hai cạnh tương ứng)
Như vậy, điểm C cách đường thẳng d cố định một khoảng cách bằng 2cm không đổi nên khi điểm B di chuyển trên đường thẳng d thì điểm C di chuyển trên đường thẳng song song với d và cách d một khoảng bằng 2cm.
Kẻ AH và CK vuông góc với dd.
Vì C là điểm đối xứng với A qua B (gt)
⇒AB=CB (tính chất hai điểm đối xứng qua 1 điểm)
Xét hai tam giác vuông AHB và CKB có:
AB=CB (cmt)
\(\widehat{ABH}=\widehat{CBK}\) ( đối đỉnh)
nên ∆AHB=∆CKB (cạnh huyền - góc nhọn)
⇒ CK=AH=2cm (2 cạnh tương ứng)
Điểm C cách đường thẳng d cố định một khoảng cách không đổi 2cm nên C di chuyển trên đường thẳng m song song với d và cách d một khoảng bằng 2cm.