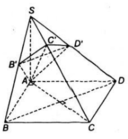
Cho S.ABCD có đáy ABCD là hình vuông cạnh a, SA = a căn 2. Tính d(AC,SD) và d(BD,SC)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
21 tháng 3 2023
Sửa đề; SA=SB=SC=SD=2a
SA=SB
OA=OB
=>SO là trung trực của AB
=>SO vuông góc AB(2)
SA=SD
OA=OD
=>SO là trung trực của AD
=>SO vuông góc AD(1)
Từ (1), (2) suy ra SO vuông góc (ABCD)
(SC;(ABCD))=(CS;CO)=góc SCO
\(OC=\dfrac{a\sqrt{2}}{2}\)
\(SO=\sqrt{SA^2+AO^2}\)
\(=\sqrt{\left(2a\right)^2+\left(\dfrac{a\sqrt{2}}{2}\right)^2}=\sqrt{4a^2+\dfrac{1}{2}a^2}=\dfrac{3}{\sqrt{2}}a\)
\(SC=\sqrt{SO^2+OC^2}=\sqrt{\dfrac{9}{2}a^2+\dfrac{1}{2}a^2}=a\sqrt{5}\)
\(cosSCO=\dfrac{OC}{SC}\)
\(=\dfrac{a\sqrt{2}}{2}:a\sqrt{5}=\dfrac{\sqrt{2}}{2\sqrt{5}}\)
=>\(\widehat{SCO}\simeq72^0\)
=>\(\left(SC;\left(ABCD\right)\right)=72^0\)
CM
16 tháng 8 2017
Đáp án D.
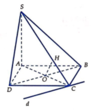
Trong mp A B C D gọi O là giao điểm của AC và BD.
Trong mặt phẳng S A C , qua O kẻ đường thẳng vuông góc với SC, cắt SC tại H.
Ta có B D ⊥ A C B D ⊥ S A ⇒ B D ⊥ S A C ⇒ B D ⊥ O H ⇒ O H là đường vuông góc chung của hai đường thẳng SC và BD.
Lại có A C = a 2 ⇒ C S = S A 2 + A C 2 = a 2 + 2 a 2 = 3 a 2 = a 3 .
Hai tam giác COH và CSA đồng dạng với nhau. Suy ra
O H S A = C O C S ⇒ O H = S A . C O C S = a . a 2 2 a 3 = a 6 6
Vậy khoảng cách giữa hai đường thẳng SC và BD bằng a 6 6 .
Chọn đáp án D.
15 tháng 6 2023
a: CD vuông góc AD; CD vuông góc SA
=>CD vuông góc (SAD)
b: BD vuông góc AC; BD vuông góc SA
=>BD vuông góc (SAC)
=>(SBD) vuông góc (SAC)
17 tháng 6 2023
a: SO vuông góc (ABCD)
=>(SAC) vuông góc (ABCD)
SO vuông góc (ABCD)
=>(SBD) vuông góc (ABCD)
b: BD vuông góc AC
BD vuông góc SA
=>BD vuông góc (SAC)
d: (SB;(ABCD))=(BS;BO)=góc SBO
cos SBO=OB/SB=a*căn 2/2/(a*căn 2)=1/2
=>góc SBO=60 độ
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 4 2022
Đề bài thiếu dữ liệu liên quan vị trí đỉnh S. Ví dụ SA có vuông góc đáy hay không?
