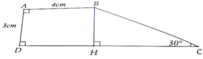
Cho tứ giác ABCD có A=D=90o, C=40o, AB=4cm, AD=3cm. Tính diện tích tứ giác
Vẽ hình giúp
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
25 tháng 10 2017
Kẻ BH ⊥ DC tại H. Chú ý diện tích ABCD bằng tổng diện tích của ABHD và BHC
CM
27 tháng 6 2019
hay ABCD là hình thang vuông tại A, D
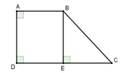
Kẻ BE ⊥ DC tại E
Tứ giác ABED có ba góc vuông A ^ = D ^ = 90 0 nên ABED là hình chữ nhật
Suy ra DE = AB = 4cm; BE = AD = 3cm
Xét tam giác BEC vuông tại E có:
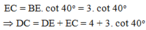
Do đó SABCD = A B + C D . A D 2 = 4 + 4 + 3. cot 40 o .3 2 = 17 , 36 c m 2
Đáp án cần chọn là: A
15 tháng 8 2015
kẻ đường cao BH
xét tứ giác ABHD có góc A=góc D=góc H=90 độ
=> ABHD là hình chữ nhật
=> S ABHD=AB.AD=4.3=12 cm vuông
xét tam giác vuông BHC có tanC=BH/HC =>HC=BH/tanC=3/tan\(40^0\)=3.6 cm
=> S BHC=1/2.BH. HC=1/2.3.3,6=5,4 cm vuông
=> S ABCD= S ABHC+S BHC=12+5,4=17,4 cm vuông
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 9 2021
1.
\(A+B+C=180^0\Rightarrow A=180^0-\left(B+C\right)=70^0\)
Kẻ đường cao BD
Trong tam giác vuông ABD:
\(cotA=\dfrac{AD}{BD}\Rightarrow AD=BD.cotA\)
Trong tam giác vuông BCD:
\(cotC=\dfrac{CD}{BD}\Rightarrow CD=BD.cotC\)
\(\Rightarrow AD+CD=BD.cotA+BD.cotC\)
\(\Rightarrow AC=BD.\left(cotA+cotC\right)\)
\(\Rightarrow BD=\dfrac{AC}{cotA+cotC}\)
\(\Rightarrow S_{ABC}=\dfrac{1}{2}BD.AC=\dfrac{1}{2}.\dfrac{AC^2}{cotA+cotC}=\dfrac{35^2}{2\left(cot70^0+cot50^0\right)}\approx509,1\left(cm^2\right)\)
NT
2
19 tháng 8 2017
kẻ đường cao BH
xét tứ giác ABHD có góc A=góc D=góc H=90 độ
=> ABHD là hình chữ nhật
=> S ABHD=AB.AD=4.3=12 cm vuông
xét tam giác vuông BHC có tanC=BH/HC =>HC=BH/tanC=3/tan400=3.6 cm
=> S BHC=1/2.BH. HC=1/2.3.3,6=5,4 cm vuông
=> S ABCD= S ABHC+S BHC=12+5,4=17,4 cm vuông
Từ B kẻ BH⊥CD
⇒ ABHD là hình chữ nhật
⇒ \(\left\{{}\begin{matrix}HD=AB=4cm\\BH=AD=3cm\end{matrix}\right.\)
Ta được: \(HC=\dfrac{BH}{tan30^0}=\dfrac{3}{\dfrac{\sqrt{3}}{3}}=3\sqrt{3}\) ( cm )
⇒ CD = HC + HD = 4 + \(3\sqrt{3}\) cm
Khi đó:
\(S_{ABCD}=\dfrac{1}{2}\left(AB+CD\right)AD=\dfrac{1}{2}\left(4+4+3\sqrt{3}\right).3\)
⇔ \(S_{ABCD}=\dfrac{24+9\sqrt{3}}{2}\) \(\left(cm^2\right)\)
chỉ vậy ai hiểu