Cho hình chóp S.ABCD có đấy là hình thoi cạnh a, góc BAD= 60 độ. SA vuông với (ABCD). d(A,SC)=a. Tính Vc, d(A,(SBC)), d(SB,AC).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 6 2021
Dễ dàng chứng minh \(BD\perp\left(SAC\right)\Rightarrow BD\perp SC\)
Gọi O là tâm đáy, kẻ \(OH\perp SC\Rightarrow SC\perp\left(BDH\right)\)
\(\Rightarrow\widehat{BHD}\) hoặc góc bù của nó là góc giữa (SBC) và (SCD) \(\Rightarrow\widehat{BHD}=60^0\) hoặc \(120^0\)
\(\Rightarrow\widehat{BHO}\) bằng \(30^0\) hoặc \(60^0\)
Tam giác ABD đều \(\Rightarrow BD=a\) \(\Rightarrow OB=\dfrac{a}{2}\)
TH1: \(\widehat{BHO}=30^0\)
\(\Rightarrow OH=\dfrac{OB}{tan30^0}=\dfrac{a\sqrt{3}}{2}=OC\Rightarrow\Delta\) vuông OCH có cạnh huyền bằng cạnh góc vuông (loại)
TH2: \(\widehat{BHO}=60^0\Rightarrow OH=\dfrac{OB}{tan60^0}=\dfrac{a\sqrt{3}}{6}\)
\(\Rightarrow SA=AC.tan\widehat{SCA}=AC.\dfrac{OH}{\sqrt{OC^2-OH^2}}=\dfrac{a\sqrt{6}}{4}\)
Từ A kẻ \(AM\perp SB\Rightarrow AM\perp\left(SBC\right)\Rightarrow AM=d\left(A;\left(SBC\right)\right)\)
\(AD||BC\Rightarrow AD||\left(SBC\right)\Rightarrow d\left(BK;AD\right)=d\left(AD;\left(SBC\right)\right)=d\left(A;\left(SBC\right)\right)=AM\)
\(\dfrac{1}{AM^2}=\dfrac{1}{SA^2}+\dfrac{1}{AB^2}=\dfrac{11}{3a^2}\Rightarrow AM=\dfrac{a\sqrt{33}}{11}\)
CM
19 tháng 4 2019
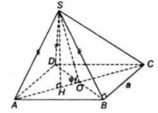
a) Tam giác ABD có AB = AD ( do ABCD là hình thoi)
=> Tam giác ABD cân tại A. Lại có góc A= 60o
=> Tam giác ABD đều.
Lại có; SA = SB = SD nên hình chóp S.ABD là hình chóp đều.
* Gọi H là tâm của tam giác ABD
=>SH ⊥ (ABD)
*Gọi O là giao điểm của AC và BD.
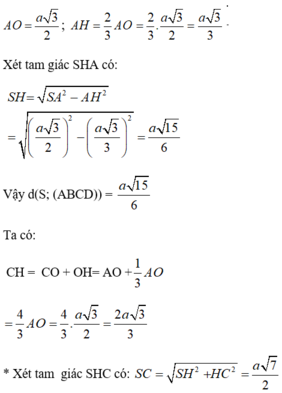
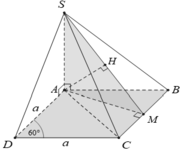
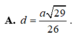
Lời giải:
Tính toán đơn giản: \(AC=\sqrt{3}a, DB=a\)
Ý 1:
Do \(SA\perp (ABCD)\Rightarrow SA\perp AC\). Áp dụng định lý Pitago:
\( \frac{1}{d(A,SC)^2}=\frac{1}{SA^2}+\frac{1}{AC^2}\Leftrightarrow \frac{1}{a^2}=\frac{1}{SA^2}+\frac{1}{3a^2}\Rightarrow SA=\frac{\sqrt{6}}{2}a\)
\(\Rightarrow V_{\text{chóp}}=\frac{1}{3}.SA.S_{ABCD}=\frac{1}{3}.\frac{\sqrt{6}a}{2}.\frac{AC.BD}{2}=\frac{\sqrt{2}a^3}{4}\)
Ý 2:
Kẻ \(AH\perp BC\) với \(H\in BC\). Có \(\left\{\begin{matrix} AH\perp BC\\ SA\perp BC\end{matrix}\right.\Rightarrow BC\perp (SAH)\)
Kẻ \(AT\perp SH\), mà \(AT\perp BC\) do \(AT\in (SAH)\) , do đó \(AT\perp (SBC)\)
\(\Rightarrow AT=d(A,(SBC))=\sqrt{\frac{SA^2.AH^2}{SA^2+AH^2}}\)
Mà \(AH=\sin 60.AB=\frac{\sqrt{3}a}{2}\), suy ra \(d(A,(SBC))=AT=\frac{\sqrt{2}a}{2}\)
Ý 3:
Kẻ \(BK\parallel AC\) cắt $AD$ tại $K$
Ta có: \(d(SB,AC)=d(AC,(SBK))=d(A,(SBK))\)
Kẻ \(AR\perp BK\).
Có \(AR=AB.\sin ABK=AB.\sin BAC=AB\sin 30=\frac{a}{2}\)
Kẻ \(AM\perp SR\) thì $AM$ chính là khoảng cách từ $A$ đến $(SBK)$
\(d(A,(SBK))=AM=\sqrt{\frac{SA^2.AR^2}{SA^2+AR^2}}=\frac{\sqrt{42}a}{14}\)