hai gương phẳng G1 và G2 đặt vuông góc với nhau chiếu 1 chùm tia sáng hẹp SI tới gương G1 với goc tới bằng 30 độ sau khi phản xạ lần lượt trên hai gương thu được chùm tia sáng phản xạ Jk song song với SI khi đó góc phản xạ tại gương G2 có giá trị là ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
20 tháng 12 2016
bn nhìn thấy Δ vuông có góc 60 va 30 thi suy ra góc giua phap tuyen voi tia toi hay tia pxa cua G2 = 60, đúng k? viêt chữ vào hình lâu lắm mà mk phải làm giúp nhiu bn khác
13 tháng 3 2022
Khi \(G_2\) quay một góc \(\beta\) thì tia phản xạ \(JR\) cũng quay một góc bằng nó \(\beta=60^o\)
K
5 tháng 3 2017
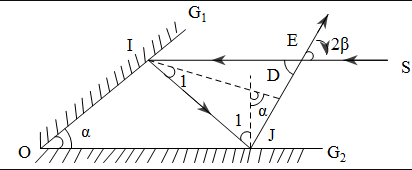
Ta có:
\(\widehat{NIJ}=\widehat{SIN}=75^o\)
\(\widehat{OIJ}=\widehat{NIO}-\widehat{NIJ}\)
\(\Rightarrow\widehat{OIJ}=90^o-75^o\)
\(\Rightarrow\widehat{OIJ}=15^o\)
\(\widehat{IJO}+\alpha+\widehat{OIJ}=180^o\) (tổng 3 góc trong 1 tam giác)
\(\Rightarrow\widehat{IJO}=180^o-\alpha-\widehat{OIJ}\)
\(\Rightarrow\widehat{IJO}=180^o-150^o-15^o\)
\(\Rightarrow\widehat{IJO}=15^o\)
\(\widehat{IJM}=\widehat{OJM}-\widehat{IJO}\)
\(\Rightarrow\widehat{IJM}=90^o-15^o\)
\(\Rightarrow\widehat{IJM}=75^o\)
Vậy góc tới gương G2 bằng 75o
31 tháng 5 2016
Giả sử tia tới là SI có góc tới là α độ, góc phản chiếu cũng bằng α, do hai gưong đặt vuông góc với nhau nên pháp tuyến ở guơg G1 và pháp tuyến ở guơng G2 vuông góc với nhau, tia phản xạ ở guơng G1 chính là tia tới ở guơng G2 hai góc này phụ nhau.(vẽ hình ra thấy). Ta được số đo góc tới ở guơng G2 là (90-α) độ, và góc phản chiếu = góc tới nên góc phản chiếu ở G2 = (90 - α) độ.
Tia tới ở G2 là tia IK thì từ một điểm bất kỳ M trên tia phản xạ Kt ở gưong G2 ta kẻ đừong thẳng song song với IK cắt tia SI ở H thì tứ giác HIKM là hình thoi vì có các cạnh song song với nhau và hai đường chéo vuông góc với nhau) Nên tia Kt và tia IK song song với nhau vậy góc phải tìm có giá trị bằng 0.
Có thể nói gọn thế này: pháp tuyến ở guơng G2 song với guơng G1 . Nên tia phản chiếu ở G2 cũng song song với tia tới SI ở G1.
* Kết luận là góc tạo bởi tia SI và tia phản xạ cuối cùng trên guơng G2 có giá trị bằng 0 độ.
Chúc bạn học tốt!!!
31 tháng 5 2016
- Giả sử tia tới là SI có góc tới là α độ, góc phản chiếu cũng bằng α, do hai gưong đặt vuông góc với nhau nên pháp tuyến ở guơg G1 và pháp tuyến ở guơng G2 vuông góc với nhau, tia phản xạ ở guơng G1 chính là tia tới ở guơng G2 hai góc này phụ nhau. Ta được số đo góc tới ở guơng G2 là (90-α) độ, và góc phản chiếu = góc tới nên góc phản chiếu ở G2 = (90-α) độ.
- Tia tới ở G2 là tia IK thì từ một điểm bất kỳ M trên tia phản xạ Kt ở gưong G2 ta kẻ đừong thẳng song song với IK cắt tia SI ở H thì tứ giác HIKM là hình thoi vì có các cạnh song song với nhau và hai đường chéo vuông góc với nhau) nên tia Kt và tia IK song song với nhau vậy góc phải tìm có giá trị bằng 0.
- Có thể nói gọn thế này : pháp tuyến ở guơng G2 song với guơng G1. Nên tia phản chiếu ở G2 cũng song song với tia tới SI ở G1.
- Kết luận là góc tạo bởi tia SI và tia phản xạ cuối cùng trên guơng G2 có giá trị bằng 0 độ.
Chúc bạn học tốt!!!
24 tháng 6 2016
Góc tạo bởi tia tới SI và tia phản xạ cuối cùng trên gương G2 có giá trị là 0o.
Vậy chọn A.
24 tháng 6 2016
Để bik thêm chi tiết, xin zui lòng lật sách BTVL7, trg 14, câu 4.10
ST
20 tháng 12 2021
Giả sử tia tới là SI có góc tới là: \(i=\widehat{SIN}=a\)
Định luật phản xạ tại gương \(G_1:\) \(\widehat{SIN}=\widehat{NIR}=a\left(1\right)\)
Do hai gương đặt song song với nhau nên pháp tuyến IN ở gương \(G_1\) và pháp tuyến \(RN'\) ở gương \(G_2\) song song với nhau, tia phản xạ ở \(G_1\) chính là tia tới ở gương \(G_2\) : \(\widehat{N'RI}=\widehat{RIN}=a\)
Định luật phản xạ tại gương \(G_2\) : \(\widehat{IRN}'=\widehat{N'RK}=a\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\) ta có: \(\widehat{SIR}=\widehat{IRK}=2a\)
Vì hai góc này so le trong nên SI // RK. Nên góc tạo bởi tia tới SI và tia phản xạ cuối cùng trên gương \(G_2\) có giá trị \(0^o\)
\(\Rightarrow ChọnA\)
TH
25 tháng 11 2021
a, Đầu tiên vẽ tia tới chiếu đến gương G1 tại I, rồi phản đến gương G2 tại điểm I' , rồi phản xạ tiếp qua điểm R
b, Ta có tia pháp tuyến \(NI\perp I\) (G1) , \(NI'\perp I'\left(G2\right)\)
mà 2 gương G1 , G2 vuông góc vói nhau
\(\Rightarrow\left\{{}\begin{matrix}i=90^o-45^o=45^o\\i=i'\Leftrightarrow i'=45^o\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}i2=90^o-45^o=45^o\\i2=i2'\Leftrightarrow i2'=45^o\end{matrix}\right.\)
Góc tạo bởi tia tới SI và tia phản xạ cuối cùng trên gương G2 : \(45^o+45^o+45^o+45^o=180^o\)
25 tháng 11 2021
Tham khảo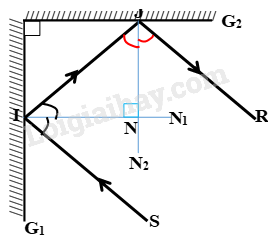
Do hai gương đặt vuông góc với nhau nên hai pháp tuyến IN1IN1 và JN2JN2 cũng vuông góc với nhau.
Định luật phản xạ tại gương G1G1:
ˆSIN=ˆNIJ⇒ˆSIJ=2ˆNIJ(1)SIN^=NIJ^⇒SIJ^=2NIJ^(1)
Định luật phản xạ tại gương G2G2:
ˆIJN=ˆNJR⇒ˆIJR=2ˆIJN(2)IJN^=NJR^⇒IJR^=2IJN^(2)
ΔIJNΔIJN vuông tại NN:
ˆNIJ+ˆNJI=900NIJ^+NJI^=900
⇒ˆSIJ+ˆIJR=2ˆNIJ+2ˆNJI=2(ˆNIJ+ˆNJI)=1800⇒SIJ^+IJR^=2NIJ^+2NJI^=2(NIJ^+NJI^)=1800
Vậy tia tới SISI song song với tia phản xạ JRJR. Góc tạo bởi tia tới SISI và tia phản xạ cuối cùng trên gương G2G2 có giá trị 1800
Ta có:
\(\widehat{SIJ}=2\widehat{SIN}=2\cdot30^o=60^o\)
SI // JK \(\Rightarrow\widehat{SIJ}+\widehat{IJK}=180^o\) (2 góc bù nhau)
\(\Rightarrow\widehat{IJK}=180^o-\widehat{SIJ}\)
\(\Rightarrow\widehat{IJK}=180^o-60^o\)
\(\Rightarrow\widehat{IJK}=120^o\)
\(\Rightarrow\widehat{MJK}=\dfrac{\widehat{IJK}}{2}=\dfrac{120^o}{2}=60^o\)
Vậy...