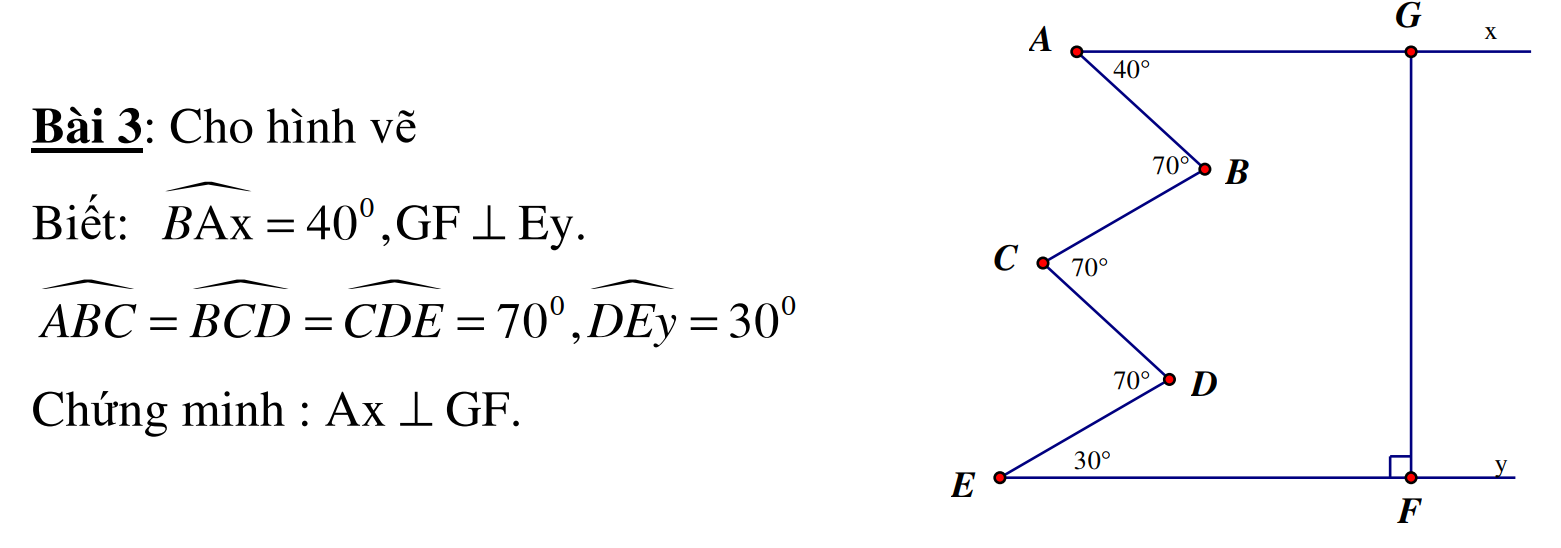
Mình đag cần rất rất gấp trc 4h30. mọi ng giúp mình vớiiiiiiiiiii. Giúpppppppppppppp
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TA
0
TV
15 tháng 8 2021
A=/x-1/+/x-3/+/x-5/+/x-7/=/x-1/+/3-x/+/x-5/+/7-x/>=/x-1+3-x/+/x-5+7-x/=4
dấu "=" xảy ra khi và chỉ khi \(\hept{\begin{cases}x-1>=0,3-x>=0\\x-5>=0,7-x>=0\end{cases}\Rightarrow\hept{\begin{cases}x>=1,3>=x\\x>=5,7>=x\end{cases}\Rightarrow}\hept{\begin{cases}1< =x< =3\\5< =x< =7\end{cases}}}\)
vậy 1<=x<=3 và 5<=x<=7
TA
1
NM
Nguyễn Minh Quang
Giáo viên
14 tháng 8 2021
ta có
\(\hept{\begin{cases}\left|x-1\right|+\left|x-7\right|\ge\left|x-1-x+7\right|=6\\\left|x-3\right|\ge0\end{cases}}\)
Vậy \(A\ge6\) dấu bằng xảy ra khi x=3
TA
1
NM
Nguyễn Minh Quang
Giáo viên
12 tháng 8 2021
DỰng thêm đường DG,CH song song vơi AB như hình vẽ
ta có : \(\widehat{HCD}=\widehat{DCA}-\widehat{HCA}=110^0-90^0=30^0\)
mà ta có \(\hept{\begin{cases}\widehat{HCD}=\widehat{CDG}=30^0\\\widehat{GDE}=\widehat{DÈF}=30^0\end{cases}}\Rightarrow\widehat{CDE}=\widehat{CDG}+\widehat{GDE}=30^0+30^0=60^0\)
TA
0
TA
1
11 tháng 8 2021
Ta có : \(\left|x-2\right|+\left|y-5\right|+10\ge10\)
\(\Rightarrow\frac{-15}{\left|x-2\right|+\left|y-5\right|+10}\ge-\frac{15}{10}=-\frac{3}{2}\)
\(\Rightarrow B=3-\frac{15}{\left|x-2\right|+\left|y-5\right|+10}\ge3-\frac{3}{2}=\frac{3}{2}\)
Dấu ''='' xảy ra khi x = 2 ; y = 5
Vậy GTNN của B bằng 3/2 tại x = 2 ; y = 5
TA
0
TA
2
11 tháng 8 2021
tìm GTNN hả bạn ?
\(A=1,7+\left|3,4-x\right|\ge1,7\)
Dấu ''='' xảy ra khi x = 3,4
Vậy GTNN của A bằng 1,7 tại x = 3,4
