a) \(\dfrac{3}{4}+x=\dfrac{8}{13}\)
b) \(\dfrac{11}{12}-\left(\dfrac{2}{5}+x\right)=\dfrac{2}{3}\)
c)\(2x\left(x-\dfrac{1}{7}\right)=0\)
d)\(\dfrac{3}{4}+\dfrac{1}{4}:x=\dfrac{2}{5}\)
\(\dfrac{3}{4}+x=\dfrac{8}{13}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: (x+1/2)(2/3-2x)=0
=>x+1/2=0 hoặc 2/3-2x=0
=>x=-1/2 hoặc x=1/3
b: 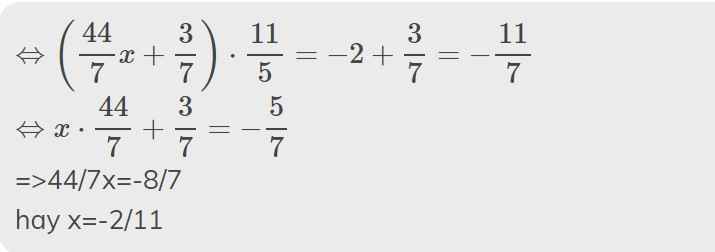
c: \(\Leftrightarrow x\cdot\left(\dfrac{13}{4}-\dfrac{7}{6}\right)=\dfrac{5}{12}+\dfrac{5}{3}=\dfrac{5}{12}+\dfrac{20}{12}=\dfrac{25}{12}\)
\(\Leftrightarrow x=\dfrac{25}{12}:\dfrac{39-14}{12}=\dfrac{25}{25}=1\)

\(b,\Rightarrow\dfrac{x}{2}-\dfrac{3x}{5}-\dfrac{13}{5}=-\dfrac{7}{5}-\dfrac{7x}{10}\\ \Rightarrow\dfrac{1}{2}x-\dfrac{3}{5}x+\dfrac{7}{10}x=\dfrac{6}{5}\\ \Rightarrow\dfrac{3}{5}x=\dfrac{6}{5}\Rightarrow x=2\\ c,\Rightarrow\dfrac{2x-3}{3}-\dfrac{5-3x}{6}=-\dfrac{1}{3}+\dfrac{3}{2}=\dfrac{7}{6}\\ \Rightarrow\dfrac{4x-6-5+3x}{6}=\dfrac{7}{6}\\ \Rightarrow7x-11=7\Rightarrow x=\dfrac{18}{7}\\ d,\Rightarrow\dfrac{2}{3x}+\dfrac{7}{x}=\dfrac{4}{5}+2+\dfrac{3}{12}=\dfrac{61}{20}\\ \Rightarrow\dfrac{23}{3x}=\dfrac{61}{20}\\ \Rightarrow183x=460\\ \Rightarrow x=\dfrac{460}{183}\\ e,\Rightarrow2\left(x-1\right)-\left(x-1\right)^2=0\\ \Rightarrow\left(x-1\right)\left(2-x+1\right)=0\\ \Rightarrow\left[{}\begin{matrix}x=1\\x=3\end{matrix}\right.\)
e: Ta có: \(\left(x-1\right)^2=2\left(x-1\right)\)
\(\Leftrightarrow\left(x-1\right)\left(x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=3\end{matrix}\right.\)

\(a,\left(x-2\right)\left(x-3\right)-3\left(4x-2\right)=\left(x-4\right)^2\\ \Leftrightarrow x^2-5x+6-12x+6=x^2-8x+16\\ \Leftrightarrow-9x-4=0\\ \Leftrightarrow x=-\dfrac{4}{9}\)
\(b,\dfrac{2x^2+1}{8}-\dfrac{7x-2}{12}=\dfrac{x^2-1}{4}-\dfrac{x-3}{6}\\ \Leftrightarrow6x^2+3-14x+4=6x^2-6-4x+12\\ \Leftrightarrow10x=1\\ \Leftrightarrow x=\dfrac{1}{10}\)
\(c,x-\dfrac{2x-2}{5}+\dfrac{x+8}{6}=7+\dfrac{x-1}{3}\\ \Leftrightarrow30x-12x+12+5x+40=210+10x-10\\ \Leftrightarrow13x=148\\ \Leftrightarrow x=\dfrac{148}{13}\)
\(d,\left(2x+5\right)^2=\left(x+2\right)^2\\ \Leftrightarrow\left(2x+5\right)^2-\left(x+2\right)^2=0\\ \Leftrightarrow\left(2x+5-x-2\right)\left(2x+5+x+2\right)=0\\ \Leftrightarrow\left(x+3\right)\left(3x+7\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=-3\\x=-\dfrac{7}{3}\end{matrix}\right.\)
\(e,x^2-5x+6=0\\ \Leftrightarrow\left(x-2\right)\left(x-3\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=2\\x=3\end{matrix}\right.\)
\(g,2x^3+6x^2=x^2+3x\\ \Leftrightarrow2x^2\left(x+3\right)-x\left(x+3\right)=0\\ \Leftrightarrow x\left(2x-1\right)\left(x+3\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{1}{2}\\x=-3\end{matrix}\right.\)
\(h,\left(x+\dfrac{1}{x}\right)^2+2\left(x+\dfrac{1}{x}\right)-8=0\left(x\ne0\right)\)
Đặt \(x+\dfrac{1}{x}=t\), pt trở thành:
\(t^2+2t-8=0\\ \Leftrightarrow\left(t-2\right)\left(t+4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}t=2\\t=-4\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x+\dfrac{1}{x}=2\\x+\dfrac{1}{x}=-4\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x^2+1-2x=0\\x^2+1+4x=0\left(1\right)\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}\left(x-1\right)^2=0\\\Delta\left(1\right)=16-4=12>0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=1\\\left[{}\begin{matrix}x=-2+\sqrt{3}\\x=-2-\sqrt{3}\end{matrix}\right.\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=1\\x=-2+\sqrt{3}\\x=-2-\sqrt{3}\end{matrix}\right.\)
Tick plzz

\(a)\left(\dfrac{1}{2}+1,5\right)x=\dfrac{1}{5}\)
\(\Rightarrow2x=\dfrac{1}{5}\)
\(\Rightarrow x=\dfrac{1}{10}\)
\(b)\left(-1\dfrac{3}{5}+x\right):\dfrac{12}{13}=2\dfrac{1}{6}\)
\(\Leftrightarrow-\dfrac{8}{5}+x=\dfrac{13}{6}.\dfrac{12}{13}\)
\(\Leftrightarrow-\dfrac{8}{5}+x=2\)
\(\Leftrightarrow x=\dfrac{18}{5}\)
\(c)\left(x:2\dfrac{1}{3}\right).\dfrac{1}{7}=-\dfrac{3}{8}\)
\(\Leftrightarrow x:\dfrac{7}{3}=-\dfrac{3}{8}:\dfrac{1}{7}\)
\(\Leftrightarrow x=-\dfrac{21}{8}.\dfrac{7}{3}\)
\(\Leftrightarrow x=-\dfrac{49}{8}\)
\(d)-\dfrac{4}{7}x+\dfrac{7}{5}=\dfrac{1}{8}:\left(-1\dfrac{2}{3}\right)\)
\(\Leftrightarrow-\dfrac{4}{7}x+\dfrac{7}{5}=-\dfrac{3}{40}\)
\(\Leftrightarrow-\dfrac{4}{7}x=-\dfrac{59}{40}\)
\(\Leftrightarrow x=\dfrac{413}{160}\)

a: =>1/2x=7/2-2/3=21/6-4/6=17/6
=>x=17/3
b: =>2/3:x=-7-1/3=-22/3
=>x=2/3:(-22/3)=-1/11
c: =>1/3x+2/5x-2/5=0
=>11/15x=2/5
hay x=6/11
d: =>2x-3=0 hoặc 6-2x=0
=>x=3/2 hoặc x=3

a: =>x-3/4=1/6-1/2=1/6-3/6=-2/6=-1/3
=>x=-1/3+3/4=-4/12+9/12=5/12
b: =>x(1/2-5/6)=7/2
=>-1/3x=7/2
hay x=-21/2
c: (4-x)(3x+5)=0
=>4-x=0 hoặc 3x+5=0
=>x=4 hoặc x=-5/3
d: x/16=50/32
=>x/16=25/16
hay x=25
e: =>2x-3=-1/4-3/2=-1/4-6/4=-7/4
=>2x=-7/4+3=5/4
hay x=5/8

a) \(\dfrac{11}{10}+\dfrac{3}{5}:\dfrac{2}{3}=\dfrac{11}{10}+\dfrac{3}{5}\times\dfrac{3}{2}=\dfrac{11}{10}+\dfrac{9}{10}=\dfrac{20}{10}=2\)
b) \(\dfrac{4}{3}+5\times\dfrac{5}{8}=\dfrac{4}{3}+\dfrac{25}{8}=\dfrac{32}{24}+\dfrac{75}{24}=\dfrac{107}{24}\)
c) \(\left(\dfrac{2}{5}+\dfrac{3}{7}\right)\times\dfrac{25}{29}=\left(\dfrac{14}{35}+\dfrac{15}{35}\right)\times\dfrac{25}{39}=\dfrac{29}{35}\times\dfrac{25}{39}=\dfrac{145}{274}\)
d) \(\dfrac{1}{4}\times\dfrac{5}{12}+\dfrac{5}{12}\times\dfrac{4}{5}=\dfrac{5}{12}\times\left(\dfrac{1}{4}+\dfrac{4}{5}\right)=\dfrac{5}{12}\times\dfrac{21}{20}=\dfrac{105}{240}=\dfrac{7}{16}\)
a) \(\dfrac{11}{10}+\dfrac{3}{5}x\dfrac{3}{2}=\dfrac{11}{10}+\dfrac{9}{10}=\dfrac{20}{10}=2\)
b) \(\dfrac{4}{3}+\dfrac{25}{8}=\dfrac{32}{24}+\dfrac{75}{24}=\dfrac{107}{24}\)
c) \(\dfrac{29}{35}x\dfrac{25}{29}=\dfrac{5}{7}\)
\(=\dfrac{5}{12}x\left(\dfrac{1}{4}+\dfrac{4}{5}\right)=\dfrac{5}{12}x\dfrac{21}{20}=\dfrac{7}{16}\)

a: \(=\dfrac{-6}{11}:\dfrac{3\cdot11}{4\cdot5}=\dfrac{-6}{11}\cdot\dfrac{20}{33}=\dfrac{-2}{11}\cdot\dfrac{20}{11}=\dfrac{-40}{121}\)
b: \(=\dfrac{7}{12}+\dfrac{5}{72}-\dfrac{11}{36}=\dfrac{42}{72}+\dfrac{5}{72}-\dfrac{22}{72}=\dfrac{25}{72}\)
c: \(=\dfrac{13}{10}:\dfrac{-5}{13}=\dfrac{-169}{50}\)

1, \(x\left(x+\dfrac{2}{3}\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x+\dfrac{2}{3}=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{-2}{3}\end{matrix}\right.\)
2, a, \(\left|x+\dfrac{4}{6}\right|\ge0\)
Để \(\left|x+\dfrac{4}{6}\right|\) đạt GTNN thì \(\left|x+\dfrac{4}{6}\right|=0\)
\(\Leftrightarrow x+\dfrac{4}{6}=0\Rightarrow x=\dfrac{-2}{3}\)
Vậy, ...
b, \(\left|x-\dfrac{1}{3}\right|\ge0\)
Để \(\left|x-\dfrac{1}{3}\right|\) đạt GTLN thì \(\left|x-\dfrac{1}{3}\right|=0\)
\(\Leftrightarrow x-\dfrac{1}{3}=0\Rightarrow x=\dfrac{1}{3}\)
Vậy, ...
1)
a)
\(x\cdot\left(x+\dfrac{2}{3}\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\x+\dfrac{2}{3}=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=0\\x=-\dfrac{2}{3}\end{matrix}\right.\)
2)
a)
\(\left|x+\dfrac{4}{6}\right|\ge0\)
Dấu \("="\) xảy ra khi \(x+\dfrac{4}{6}=0\Leftrightarrow x=\dfrac{-4}{6}\Leftrightarrow x=\dfrac{-2}{3}\)
Vậy \(Min_{\left|x+\dfrac{4}{6}\right|}=0\text{ khi }x=\dfrac{-2}{3}\)
b)
\(\left|x-\dfrac{1}{3}\right|\ge0\)
Dấu \("="\) xảy ra khi \(x-\dfrac{1}{3}=0\Leftrightarrow x=\dfrac{1}{3}\)
Vậy \(Min_{\left|x-\dfrac{1}{3}\right|}=0\text{ khi }x=\dfrac{1}{3}\)
a, \(\dfrac{3}{4}+x=\dfrac{8}{13}\)
\(x=\dfrac{8}{13}-\dfrac{3}{4}\)
\(x=-\dfrac{7}{52}\)
b,\(\dfrac{11}{12}-\left(\dfrac{2}{5}+x\right)=\dfrac{2}{3}\)
\(\dfrac{2}{5}+x=\dfrac{11}{12}-\dfrac{2}{3}\)
\(\dfrac{2}{5}+x=\dfrac{1}{4}\)
\(x=\dfrac{1}{4}-\dfrac{2}{5}\)
\(x=-\dfrac{3}{20}\)
c, \(2x\left(x-\dfrac{1}{7}\right)=0\)
\(2x-\dfrac{1}{7}=0\)
\(x-\dfrac{1}{7}=0:2\)
\(x-\dfrac{1}{7}=0\)
\(x=0-\dfrac{1}{7}\)
\(x=\dfrac{1}{7}\)
d, \(\dfrac{3}{4}+\dfrac{1}{4}\div x=\dfrac{2}{5}\)
\(\left(\dfrac{3}{4}+\dfrac{1}{4}\right):x=\dfrac{2}{5}\)
\(1:x=\dfrac{2}{5}\)
\(x=1:\dfrac{2}{5}\)
\(x=\dfrac{5}{2}\)
a) \(\dfrac{3}{4}+x=\dfrac{8}{13}\)\(\Leftrightarrow\) \(x=\dfrac{8}{13}-\dfrac{3}{4}=\dfrac{-7}{52}\) vậy \(x=\dfrac{-7}{52}\)
b) \(\dfrac{11}{12}-\left(\dfrac{2}{5}+x\right)=\dfrac{2}{3}\) \(\Leftrightarrow\) \(\dfrac{11}{12}-\dfrac{2}{5}-x=\dfrac{2}{3}\) \(\Leftrightarrow\) \(x=\dfrac{11}{12}-\dfrac{2}{5}-\dfrac{2}{3}=\dfrac{-3}{20}\) vậy \(x=\dfrac{-3}{20}\)
c) \(2x\left(x-\dfrac{1}{7}\right)=0\) \(\Leftrightarrow\) \(2x^2-\dfrac{2}{7}x=0\)
\(\Delta\) = \(\left(\dfrac{-2}{7}\right)^2-4.2.0=\dfrac{4}{49}>0\)
\(\Rightarrow\) phương trình có 2 nghiệm phân biệt
\(x_1=\dfrac{\dfrac{2}{7}+\sqrt{\dfrac{4}{49}}}{4}=\dfrac{1}{7}\)
\(x_2=\dfrac{\dfrac{2}{7}-\sqrt{\dfrac{4}{49}}}{4}=0\)
vậy \(x=0;x=\dfrac{1}{7}\)