Cho tam giác ABC vuông tại A. Đường tròn (O) nội tiếp tam giác ABC tiếp xúc với AB, AC lần lượt tại D, E
a) Tứ giác ADOE là hình gì ? Vì sao ?
b) Tính bán kính của đường tròn (O) biết AB = 3cm, AC = 4cm ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
27 tháng 11 2021
BÀI LÀM
a, xét tứ giác ADOE có:
góc A= góc E=góc D=90O
mà ta thấy: OE=OD( bán kính = nhau)
vậy tứ giác ADOE là hình vuông (dhnb)
27 tháng 11 2021
a) Dễ thấy tứ giác AEOD là hình chữ nhật (tứ giác có 3 góc vuông).
Mà OD = OE ( cùng bằng bán kính đường tròn nội tiếp tam giác ABC).
Nên tứ giác AEOD là hình vuông.
b) Gọi H là chân đường vuông góc kẻ từ O xuống BC.
Có SΔABC=SΔOAB+SΔOBC+SΔOAC
=12 OD.AB+12 OE.AC+12 OH.BC
=12 r.(AB+AC+BC)
=12 pr ( là chu vi của tam giác , là bán kính đường tròn nội tiếp).
c) Áp dụng định lý Pi-ta-go ta có: BC=√AB2+AC2=10(cm).
Diện tích tam giác ABC là: 12 AB.AC=12 .6.8=24(cm2).
Chu vi tam giác ABC là: 6+8+10=24(cm).
Suy ra: 24=12 .24.r⇔r=2(cm).
CM
4 tháng 5 2019
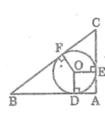
Ta có:
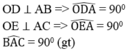
Tứ giác ADOE có ba góc vuông nên nó là hình chữ nhật
Lại có : AD = AE (tính chất hai tiếp tuyến giao nhau)
Vậy tứ giác ADOE là hình vuông
CM
17 tháng 5 2019
Áp dụng định lí Pitago vào tam giác vuông ABC ta có :
B C 2 = A B 2 + A C 2 = 3 2 + 4 2 = 25
Suy ra : BC = 5 (cm)
Theo tính chất hai tiếp tuyến giao nhau ta có:
AD = AE
BD = BF
CE = CF
Mà: AD = AB – BD
AE = AC – CF
Suy ra: AD + AE = AB – BD + (AC – CF)
= AB + AC – (BD + CF)
= AB + AC – (BF + CF)
= AB + AC – BC
Suy ra:
2 tháng 12 2016
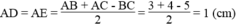
Ta có: AC = 5
Gọi bán kính đường tròn nội tiếp là r
Ta có:
S(ABC) =S(OAB) + S(OAC) +S(OBC) (1)
S(OAB) = r*AB/2
S(OAC) = r*AC/2
S(OBC) = r*BC/2
=> S(OAB) + S(OAC) +S(OBC) = r* (AB+BC+CA)/2 = 6r (2)
Mặt khác; S(ABC) = AB.AC/2 = 6 (3)
Từ (1), (2), (3) :
=> 6r = 6 => r = 1.
Ủng hộ mk nha!
12 tháng 12 2015
a, Tứ giác ADOE có 3 góc vuông => ADOE là hình chữ nhật
OE = OD ( =R ) => ADOE là hình vuông
b, Ta có R ( AB + AC + BC ) = AB . AC ( = 2. diện tích tam giác ABC )
\(BC^2=AB^2+AC^2=5^2+12^2=169=>BC=13\)
=> R ( 5+12+13) = 12 . 5 => R = 2
CM
24 tháng 8 2019
a, HS tự làm
b, HS tự làm
c, Chú ý hình thang vuông OEFO’ và xét đường trung bình của hình thang này
d, Từ I kẻ đường thảng song song với EF cắt OE tại M , cắt O’F tại N
Đặt BH=2R; CH= 2R’
∆IOM vuông tại M có:
I M 2 = I O 2 - O M 2 = R + r 2 - R - r 2 = 4 R r
Tương tự , ∆ION có I N 2 = 4 R ' r
Suy ra IM+IN=EF=AH
Vậy 2 R r + 2 R ' r = 2 R R '
=> r R + R ' = R R '
=> r = R R ' R + R ' 2
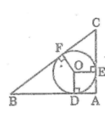
a) tứ giác ADOE là hình vuông
vì \(\left\{{}\begin{matrix}DAE=90\left(giảthiết\right)\\ODA=90\left(DlàtiếpđiểmcủađườngtrònvớiAB\right)\\OEA=90\left(Elàtiếpđiểmcủađườngtròn\:vớiAC\right)\end{matrix}\right.\)
và OD = OE = R