Trong không gian cho hai hình bình hành ABCD và AB'C'D' chỉ có chung nhau một điểm A. Chứng minh rằng các vectơ \(\overrightarrow{BB'},\overrightarrow{CC'},\overrightarrow{DD'}\) đồng phẳng ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NT
Nguyen Thuy Hoa
26 tháng 5 2017
Đúng(0)
Những câu hỏi liên quan
CM
5 tháng 1 2017
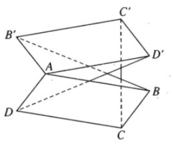
Ta có: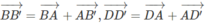 
Do đó: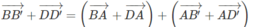 
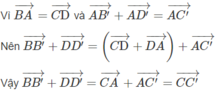
Hệ thức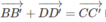 
biểu thị sự đồng phẳng của ba vectơ B B ' → , C C ' → , D D ' →
19 tháng 5 2017
\(\overrightarrow{EH}=\overrightarrow{AD},\overrightarrow{FG}=\overrightarrow{AD}\Rightarrow\overrightarrow{EH}=\overrightarrow{FG}\)
=> Tứ giác FEHG là hình bình hành
=> \(\overrightarrow{GH}=\overrightarrow{FE}\) (1)
Ta có \(\overrightarrow{DC}=\overrightarrow{AB},\overrightarrow{AB}=\overrightarrow{FE}\)
=> \(\overrightarrow{DC}=\overrightarrow{FE}\) (2)
Từ (1) và (2) ta có \(\overrightarrow{GH}=\overrightarrow{DC}\)
Vậy tứ giác GHCD là hình bình hành.
15 tháng 8 2018
1) đây nha : https://hoc24.vn/hoi-dap/question/637285.html
câu 2 cũng chả khác gì cả
