Cho tứ diện ABCD và M là điểm bất kì thuộc miền trong của tam giác BCD. Qua M kẻ các tia song song với AB, AC, AD. Các tia này theo thứ tự cắt các mặt (ACD), (ABD), (ABC) lần lượt tại B', C', D'
Chứng minh :
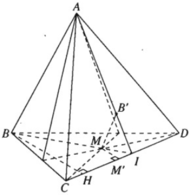
\(\dfrac{MB'}{AB}+\dfrac{MC'}{AC}+\dfrac{MD'}{AD}=1\)



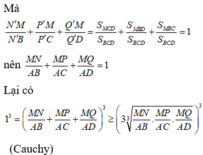



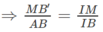
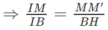
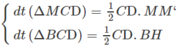
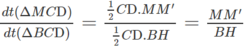
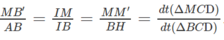
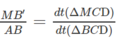
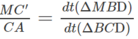
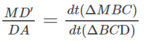
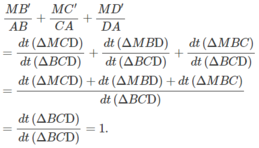
Trong tam giác ABI, ta có :
\(\dfrac{MB'}{AB}=\dfrac{MI}{BI}\left(1\right)\)