Một con lắc lò xo ngang gồm lò xo có độ cứng k=100N/m và vật m=100g, dao động trên mặt phẳng nằm ngang, hệ số ma sát giữa vật và mặt ngang là 0,02 . Kéo vật lệch khỏi vị trí cân bằng một đoạn 10cm rồi thả nhẹ cho vật dao động. Lấy g=10m/s2. Thời gian kể từ lúc bắt đầu dao động cho đến khi dừng hẳn là:
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Quãng đường của vật đi được cho đến khi dừng lại là: 

Đáp án D
Phương pháp: Sử dụng lí thuyết về bài toán dao động tắt dần của con lắc lò xo
Cách giải:
Khi vật dừng lại, toàn bộ cơ năng chuyển thành công của lực ma sát:
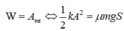
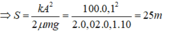

Hướng dẫn:
+ Độ biến dạng của lò xo tại vị trí cân bằng tạm x 0 = μ m g k = 0 , 1.0 , 1.10 100 = 10 − 3 m
→ Biên độ dao động của vật trong nửa chu kì đầu tiên A 1 = X 0 – x 0 .
Cứ sau mỗi nửa chu kì, kể từ nửa chu kì thứ 2 biên độ của vật dao động so với các vị trí cân bằng tạm sẽ giảm 2 x 0 .
→ Ta xét tỉ số A 1 2 x 0 = X 0 − x 0 2 x 0 = 0 , 1 − 10 − 3 2.10 − 3 = 49 , 5
→ Biên độ của vật sau 49 nửa chu kì tiếp theo là A 49 = A 1 – ( 49 . 2 + 1 ) x 0 = 1 m m → vật tắt dần tại đúng vị trí lò xo không biến dạng.
+ Áp dụng định luật bảo toàn và chuyển hóa năng lượng ta có 1 2 k X 0 2 = μ m g S → S = k X 0 2 2 μ m g = 100.0 , 1 2 2.0 , 1.0 , 1.10 = 5 m
Đáp án B

Chọn A
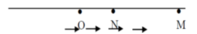
+ Vật có tốc độ cực đại khi gia tốc bằng không, tức là lúc Fhl = Fđh + Fms = 0 lần đầu tiên tại N: ON = x => kx = μmg => x = 0,02m = 2cm.
Khi đó vật đã đi được quãng đường S = MN = 6 – 2 = 4cm = 0,04m.
+ Tại x = 0: xo = 6cm = 0,06m, vo = 20√14 cm/s = 0,2√14 m/s.
Theo định luật bảo toàn năng lượng: ![]() (công của lực ma sát: μmgS).
(công của lực ma sát: μmgS).
Thay số => ![]()

Đáp án D
Biên độ A0 = 5 cm và cơ năng dao động
W
0
= ![]()
• Gọi q là công bội của cấp số nhân. Vì biên độ giảm theo cấp số nhân nên ta có:
+ Sau chu kỳ thứ 1 biên độ còn lại là: A 1 = q . A 0
+ Sau chu kỳ thứ 2 biên độ còn lại là ![]()
+ Sau chu kỳ thứ 3 biên độ còn lại là ![]()
+ Sau chu kỳ thứ 4 biên độ còn lại là ![]()
Theo giải thiết ta có
A
4
= 4cm nên ta suy được