Cho tam giác ABC có \(\widehat{B}=\widehat{C}=50^0\). Gọi Am là tia phân giác của góc ngoài ở đỉnh A. Hãy chứng tỏ rằng Am // BC ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ta có góc BAC+B+C=180 độ=> BAC=180-50-50=80 độ
ta có góc IAB=180 độ-BAC=180-80=100 độ (IAB là góc ngoài ở đỉnh A)
mà Am la pg=> IAm=mAB=IAB:2=100:2=50 độ
ta có góc IAm= góc C=50 độ ,2 góc này ở vị trí đồng vị
=> Am// BC
ta có hình vẽ:
Theo tính chất góc ngoài của tam giác , ta có: góc CAn = góc B +góc C= 50+50=100 độ
=> góc CAm= góc CAn : 2= 100 độ :2 = 50 độ
=> Am // BC ( so le trong)

cho tam giác ABC có B=C=50 độ gọi ax là tia đối của ABAM là
tia phân giác của xÁc
tính góc xac
chứng minh Am song song vs BC

Giải
= + (góc ngoài của tam giác ABC)
= 400+ 400 = 800
400.
Hai góc so le trong bằng nhau nên Ax// Bc

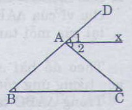
Trong Δ ABC có ∠(CAD ) là góc ngoài đỉnh A
⇒∠(CAD ) =∠B +∠C =50o+50o=100o
(tính chất góc ngoài tam giác)
∠(A1 ) =∠(A2 ) =1/2 ∠(CAD) =50o (vì tia Am là tia phân giác của ∠(CAD)
Suy ra: ∠(A1) =∠C =50o
⇒ Am // BC (vì có cặp góc ở vị trí so le trong bằng nhau)
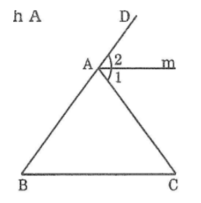

Theo đề ta giải được : \(\widehat{A}=100^0\)
Gọi à là tia phân giác ngoài của góc A .
\(\Rightarrow\widehat{A_2}=\widehat{A_3}=\frac{\left(180^0-100^0\right)}{2}=\frac{80^0}{2}=40^0\)
\(\Rightarrow\widehat{A_2}=\widehat{C}\left(=40^0\right)\)
Mà góc A 1 và góc C là hai góc so le trong .
=> Ax // BC ( đpcm )
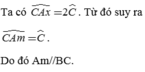
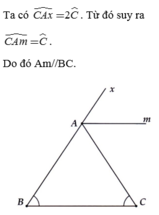
sao lại cs cả AD hả bn