Cho tam giác ABC có \(\widehat{A}=100^0\). Các đường trung trực của AB và AC lần lượt cắt BC ở E và F. Tính \(\widehat{EAF}\) ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
3 tháng 4 2018
Vì E thuộc đường trung trực của đoạn thẳng AB nên EA = EB, hay tam giác EAB cân tại đỉnh E.
Suy ra : ∠A1 = ∠B (1)
Vì F thuộc đường trung trực của đoạn thẳng AC nên FA = FC, hay tam giác FAC cân tại đỉnh F. Suy ra : ∠A2 =∠C (2).
Từ (1) và (2) suy ra: ∠A1 + ∠A2 = ∠B + ∠C
Ta có:
∠(EAF) = ∠A − (∠A1 + ∠A2 ) = ∠A − (∠B + ∠C )
Mặt khác: ∠A + ∠B + ∠C = 1800 ( tổng ba góc của một tam giác )
suy ra: ∠B + ∠C = 180o − ∠A = 180o − 100o = 80o
Do đó ∠(EAF) = 100o − 80o = 20o
9 tháng 4 2016
Đổi: 675km = 67 500 000cm
Trên bản đồ tỉ lệ 1:2 500 000 quãng đường dài là:
67 500 000 : 2 500 000 = 27 (cm)
Đáp số: 27 cm
Xin lỗi nha
7 tháng 4 2016
mk chưa hok tới đường trung trực nên ko làm được sorry !!!!
5454654
17 tháng 6 2018
Gọi M; N là ....
Ta có : \(DM\perp AB\)\(\Rightarrow\)DM là đường cao \(\Delta ABD\)
\(AM=MB\Rightarrow\)DM là trung tuyến \(\Delta ABD\)
\(\Rightarrow\Delta ABD\)cân tại D
\(\Rightarrow\widehat{BAD}=\widehat{ABD}\)
CM tương tự \(\Rightarrow\Delta AEC\)cân tại E
\(\Rightarrow\widehat{EAC}=\widehat{ACE}\)
Mà \(\widehat{BAD}+\widehat{EAC}+\widehat{DAE}=\widehat{BAC}=112^o\)
\(\Rightarrow\widehat{ABD}+\widehat{ACE}+\widehat{DAE}=112^o\left(1\right)\)
Mặt khác \(\widehat{ABC}+\widehat{ACB}+\widehat{BAC}=180^o\)
\(\Leftrightarrow\widehat{ABC}+\widehat{ACB}+112^o=180^o\)
\(\Leftrightarrow\widehat{ABC}+\widehat{ACB}=68^o\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\widehat{DAE}=44^o\)
Vậy ...
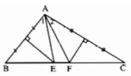
Vì E thuộc đường trung trực của đoạn thẳng AB nên EA = EB, hay tam giác EAB cân tại đỉnh E. Suy ra \(\widehat{B}=\widehat{A_1}\). Tương tự, có \(\widehat{C}=\widehat{A_2}\). Ta có:
\(\widehat{EAF}=\widehat{A}-\left(\widehat{A_1}+\widehat{A_2}\right)=\widehat{A}-\left(\widehat{B}+\widehat{C}\right)\)
Mặt khác
\(\widehat{B}+\widehat{C}=180^0-\widehat{A}=180^0-100^0=80^0\)
hong hiểu
