Trong tam giác ABC, hai đường trung tuyến \(AA_1\)và \(BB_1\) cắt nhau tại điểm O
Hãy tính diện tích tam giác ABC nếu diện tích tam giác ABO bằng \(5cm^2\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
23 tháng 5 2018
+) Vì tam giác ABC có hai đường trung tuyến AA1 và BB1 cắt nhau tại O nên O là trọng tâm tam giác ABC.
Theo tính chất trọng tâm tam giác ta có: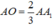 
+) Ta có: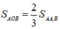 
( vì có cùng chiều cao hạ từ B và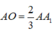 
)
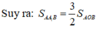
Và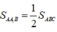 
( vì có cùng chiều cao hạ từ A và 
).
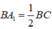+) Từ đó suy ra:
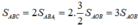
Nếu SAOB = 5cm2 thì SABC = 3.5 = 15(cm2)
Xét ΔABC có các đường trung tuyến \(AA_1;BB_1\) cắt nhau tại O
nên O là trọng tâm
=>AO=2/3AA1
\(\Leftrightarrow S_{AA_1B}=\dfrac{2}{3}S_{AOB}\)
\(\Leftrightarrow S_{ABC}=3\cdot S_{AOB}=15\left(cm^2\right)\)