Question

[Sách Giáo Khoa]

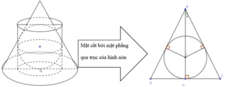
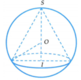
Hình 105 minh họa :

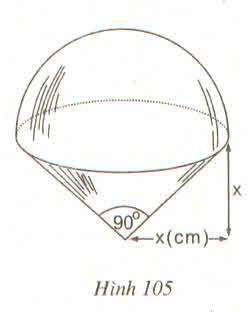
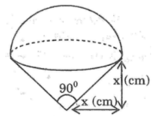
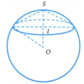
Hình gồm một nửa hình cầu và một hình nón. 

Thể tích của hình nhận giá trị nào trong các giá trị sau :

(A) \(\dfrac{2}{3}\pi x^3\left(cm^3\right)\)                            (B) \(\pi x^3\left(cm^3\right)\)

(C) \(\dfrac{4}{3}\pi x^3\left(cm^3\right)\)                            (D) \(2\pi x^3\left(cm^3\right)\)

Answer 1

[Nguyen Thuy Hoa]

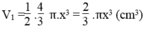
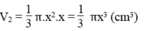
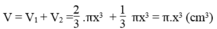
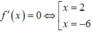
Thể tích hình nón là :

\(\dfrac{1}{3}\pi x^2.x=\dfrac{1}{3}\pi x^3\left(cm^3\right)\)

Thể tích một nửa hình cầu là :

\(\left(\dfrac{4}{3}\pi x^3\right):2=\dfrac{2}{3}\pi x^3\left(cm^3\right)\)

Vậy thể tích của hình là :

\(\dfrac{1}{3}\pi x^3+\dfrac{2}{3}\pi x^3=\pi x^3\left(cm^3\right)\)

Chọn (B)