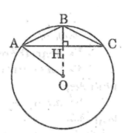
Cho tam giác cân ABC có \(\widehat{B}=120^0,AC=6cm\). Tính độ dài đường tròn ngoại tiếp tam giác đó ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NT
Nguyen Thuy Hoa
2 tháng 6 2017
Đúng(0)
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 8 2021
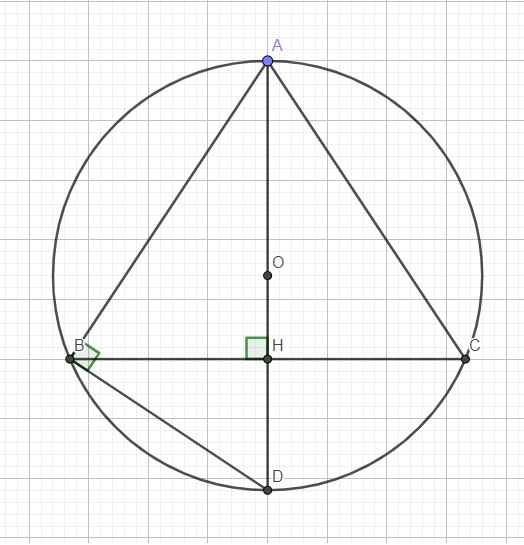
Do tam giác ABC cân tại A nên AH là đường cao đồng thời là trung trực của BC
Mà tâm của đường tròn ngoại tiếp là giao của 3 đường trung trực hay tâm O nằm trên 3 đường trung trực
\(\Rightarrow O\in AH\)
Do AD là đường kính \(\Rightarrow\widehat{ABD}\) là góc nội tiếp chắn nửa đường tròn
\(\Rightarrow\Delta ABD\) vuông tại B
Áp dụng hệ thức lượng:
\(AB^2=AH.AD\Rightarrow AD=\dfrac{AB^2}{AH}=7,2\left(cm\right)\)
ND
1
7 tháng 4 2023
\(cosA=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}\)
=>\(\dfrac{3^2+3^2-BC^2}{2\cdot3\cdot3}=-\dfrac{1}{2}\)
=>18-BC^2=-9
=>BC^2=27
=>\(BC=3\sqrt{3}\left(cm\right)\)
\(\dfrac{BC}{sinA}=2R\)
=>\(2\cdot R=3\sqrt{3}:sin120=3\sqrt{3}:\dfrac{1}{2}=6\sqrt{3}\)
=>\(R=3\sqrt{3}\)
