Một bè gỗ được thả trôi trên sông từ đập Ya-ly. Sau khi thả bè gỗ 5 giờ 20 phút, một xuồng máy cũng xuất phát từ đập Ya - ly đuổi theo và đi được 20km thì gặp bè. Tính vận tốc của bè biết rằng xuồng máy chạy nhanh hơn bè 12km/h ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NT
Nguyen Thuy Hoa
21 tháng 6 2017
Đúng(0)
Những câu hỏi liên quan
CM
11 tháng 11 2018
Gọi x (km/h) là vận tốc của bè gỗ. Điều kiện: x > 0
Khi đó vận tốc của xuồng máy là x + 12 (km/h)
thời gian bè từ lúc trôi đến lúc gặp xuồng là 20/x (giờ)
thời gian xuồng từ lúc đi đến lúc gặp bè là 20/(x + 12) (giờ)
Bè gỗ trôi trước xuồng máy 5 giờ 20 phút = 5.(1/3) (giờ) = 16/3 (giờ)
Theo đề bài, ta có phương trình:
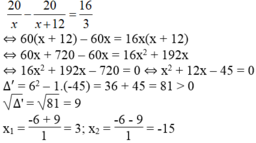
Giá trị x = -15 không thỏa mãn điều kiện bài toán.
Vậy vận tốc trôi của bè gỗ là 3km/h
2 tháng 7 2015
đổi: 6h15'=25/4
gọi vận tốc bè : x( km/h; x>0)
=> vận tốc của xuồng máy: x+10 (kmh) => vận tốc xuôi dòng: x+10+x=2x+10
thời gian xuồng đến chỗ gặp: 15/2x+10.
thời gian bè đến chỗ gặp: 15/x
vì bè đi trước 25/4 h nên ta có pt:
\(\frac{15}{x}-\frac{15}{x+10}=\frac{25}{4}\Leftrightarrow\frac{15x+150-15x}{x^2+10x}=\frac{25}{4}\Rightarrow600=25x^2+250x\Leftrightarrow x^2+10x-24=0\Leftrightarrow\left(x-2\right)\left(x+12\right)=0\)
=> x=2(t/m) hoặc x=-12(l)
=> vận tốc của bè gỗ là: 2 km/h
XO
12 tháng 1 2021
Gọi vận tốc bè gỗ là v1 (km/h) (v1 > 0)
=> Vận tốc thuyền : v1 + 4 km/h (v1 + 4 > 0)
Đổi : 3 giờ 20 phút = 10/3 giờ
Ta có v1.10/3 + v1.\(\frac{10}{v_1+4}\) = (v1 + 4).\(\frac{10}{v_1+4}\) (= 10)
=> v1.10/3 + v1.\(\frac{10}{v_1+4}\) = v1.\(\frac{10}{v_1+4}\)+ 4\(\frac{10}{v_1+4}\)
=> \(\frac{v_1.10}{3}=\frac{40}{v_1+4}\)
=> 3.40 = (v1+ 4).v1.10
=> (v1 + 4).v1 = 12
=> (v1)2 + 4.v1 - 12 = 0
=> (v1 + 2)(v1 - 6) = 0
=> \(\orbr{\begin{cases}v_1+2=0\\v_1-6=0\end{cases}}\Rightarrow\orbr{\begin{cases}v_1=-2\left(\text{loại}\right)\\v_1=6\left(tm\right)\end{cases}}\)
Vậy vận tốc của bè là 6km/h
13 tháng 7 2021
Gọi vận tốc xuồng khi nước yên lặng là \(v_1\) , vận tốc dòng nước là \(v_2\)
Vậy vận tốc bè là \(v_2\)
Vận tốc xuồng khi xuôi dòng là \(v_1+v_2\) ; khi ngược dòng là \(v_1-v_2\) và vận tốc khi xuồng hỏng là \(v_2\)
Quãng đường xuồng đi được từ khi gặp bè tới lúc bị hỏng là \(\left(v_1-v_2\right).0,25\)
Quãng đường xuồng bị trôi theo dòng nước là \(0,25v_2\)
Quãng đường đi được của xuồng kể từ khi sửa chữa xong tới lúc gặp bè lần thứ hai là \(4+\left(v_1-v_2\right)0,5-0,25v_2\)
Thời gian xuồng đi kể từ khi gặp bè lần thứ nhất tới lúc gặp bè lần thứ hai là
\(0,5+0,25+\dfrac{4+\left(v_1-v_2\right)0,5-0,25v_2}{v_1+v_2}\)
Thời gian xuồng đi kể từ khi gặp bè lần thứ nhất tới lúc gặp bè lần thứ hai là \(\dfrac{4}{v_2}\)
Thời gian đi cho tới khi gặp nhau của xuồng và bè là bằng nhau nên ta có phương trình:
\(0,5+0,25+\dfrac{4+\left(v_1-v_2\right)0,5-0,25v_2}{v_1+v_2}\) \(=\) \(\dfrac{4}{v_2}\)
Giải phương trình này ta có \(v_2=3,5\) \(km\)/\(h\)
Vậy vận tốc của dòng nước là 3,5 km/h
13 tháng 7 2021
Trong lúc làm bài có gì sai sót mong bạn bỏ qua. Nếu đúng nhớ tick cho mik nha
3 tháng 8 2017
Khôi Nguyên Hacker Man cười hơi điểu đó
a) thời gian xuôi dòng của canô là :
8 giờ 6 phút – 7 giờ 30 phút = 36 phút = 3/5 giờ.
vận tốc xuôi dòng của ca nô là :
24 : 3/5 = 40 km/h.
thời gian ngược dòng của canô là :
9 giờ 9 phút – 8 giờ 6 phút – 15 phút = 48 phút = 4/5 giờ.
vận tốc ngược dòng của ca nô là :
24 : 4/5 = 30 km/h.
b) vận tốc của dòng nước là :
(40 – 30 ) : 2 = 5 km/h.
thời gian trôi của bè gỗ từ bến A đến bến B là :
24 : 5 = 4 giờ 48 phút.
