Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
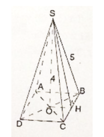
a) Ta có
OC2 = SC2 - SO2 (Pytago)
= 52 - 42 = 9(cm)
=> OC = 3(cm)
=> AC = 6(cm)
AB2 + BC2 = AC2 (pytago)
2BC2 = AC2 (do AB = BC)
BC2 = AC2/2 = 36/2 = 18(cm)
BC = √18 = 3√2 (cm)
Gọi K là trung điểm của BC. Tam giác SBC cân tại S có SH là đường trung tuyến nên SH cũng là đường cao. Suy ra SH ⊥ BC
Do đó
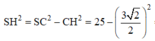
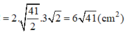
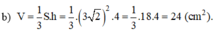
Hình chóp tứ giác đều có độ dài cạnh bên là 5cm, chiều cao 4cm.
Áp dụng định lí Pi-ta-go ta tính được nửa đường chéo của hình vuông đáy là 3 (cm)
Suy ra, đường chéo của đáy là 6 (cm)
Diện tích đáy bằng: 1/2 .6.6 = 18( c m 2 )
Thể tích của hình chóp là: V =1/3 .S.h = 1/3 .18.4 = 24 ( c m 3 )
Vậy chọn đáp án B.
Hình chóp tứ giác đều có độ dài cạnh bên là 5cm, chiều cao 4cm.
Áp dụng định lí Pi-ta-go ta tính được nửa đường chéo của hình vuông đáy là 3cm.
Suy ra, đường chéo của đáy là 6cm
Diện tích đáy bằng :
Thể tích hình chóp là:
Diện tích đáy là:
60:5=12(cm2)
ĐỘ dài cạnh đáy là căn 12=2căn 3(cm)
gọi các cạnh đáy của hình chóp là ABC vì ΔABC đều => AB=AC=BC=4cm
kẻ đường thẳng đi qua A ⊥ BC tại M
=> AM là đường cao của tam giác => \(\widehat{AMB}=\)90o
=> AM là đường trung tuyến ( tc Δ đều)
=> BM=CM=BC/2=4/2=2cm
xét ΔAMB có \(\widehat{AMB}=\)90o
=> AM2+BM2=AB2 (đl pitago)
=>AM2+22=42
=> AM=\(2\sqrt{3}\)
=> V của hình chóp = \(\dfrac{2\sqrt{3}.4}{2}.6.\dfrac{1}{3}\)=\(8\sqrt{3}\)cm3 => Đáp án B
(B) 24cm3