Tìm trên hình hộp chữ nhật \(ABCD.A_1B_1C_1D_1\) (h.113) một ví dụ cụ thể để chứng tỏ mệnh đề sau là sai :
Hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì song song với nhau.

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:AB ⊥ BC
C C 1 ⊥ BC
Nhưng AB và C C 1 không song song với nhau
Vậy mệnh đề đã cho là sai

a. Ta có: AD // BC, đường thẳng AD1 cắt AD nhưng nó không cắt BC.
Vậy mệnh đề a sai.
b. Hai đường thẳng AA1 và BC không có điểm chung nhưng chúng không song song
Vậy mệnh đề b sai.

Xét hình hộp chữ nhật A B C D . A 1 B 1 C 1 D 1
Ta có: mp(ABCD) // mp( A 1 B 1 C 1 D 1 )
AB thuộc mp(ABCD)
A 1 D 1 thuộc mp( A 1 B 1 C 1 D 1 )
AB không song song với A 1 D 1
Vậy mệnh đề đã cho sai

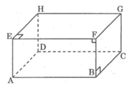
Ta có: AD // BC, đường thẳng AD1 cắt AD nhưng nó không cắt BC.
Vậy mệnh đề a) sai.

Ta có: mp(ABCD) // mp(A1B1C1D1)
AB thuộc mp(ABCD)
A1D1 thuộc mp(A1B1C1D1)
AB không song song với A1D1
Vậy mệnh đề đã cho sai.

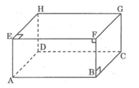 Hai đường thẳng AA1 và BC không có điểm chung nhưng chúng không song song.
Hai đường thẳng AA1 và BC không có điểm chung nhưng chúng không song song.
Vậy mệnh để b) sai.

Đáp án A
(1) Sai vì ( α ) // a ( β ) // a ( α ) ∩ ( β ) = d ⇒ a / / d tức là có trường hợp chúng cắt nhau.

a) Đúng
b) Đúng
c) Sai (vì a có thể nằm trong mp(α), xem hình vẽ)
d) Sai, chẳng hạn hai mặt phẳng (α) và (β) cùng đi qua đường thẳng a và a ⊥ mp(P) nên (α) và (β) cùng vuông góc với mp(P) nhưng (α) và (β) cắt nhau.
e) Sai, chẳng hạn a và b cùng ở trong mp(P) và mp(P) ⊥ d. Lúc đó a và b cùng vuông góc với d nhưng a và b có thể không song song nhau.
Ta có AD vuông góc với D1D vì A1D1DA là hình chữ nhật
Tương tự => DC cũng vuông góc với D1D
Mà AD chỉ vuông góc với DC vì ABCD là hình chữ nhật mà thôi chứ không song song
=> Mệnh đề trên là sai
(>Tích đúng cho mình nha<)